Chromatography stands as a fundamental technique in the scientific analysis of mixtures. It leverages different theories to enhance the separation of substances, among which Rate Theory and Plate Theory are pivotal. These theories provide frameworks to understand how components of a mixture separate under various conditions, aiding in the refinement and development of chromatographic methods.
Rate Theory and Plate Theory offer distinct perspectives on the chromatographic process. Rate Theory focuses on the kinetic processes governing the migration of molecules through a chromatographic system, emphasizing factors like diffusion and mass transfer. On the other hand, Plate Theory conceptualizes the column as a series of discrete, theoretical plates or layers, each representing an equilibrium stage of mass transfer.
These theories not only guide the design and operation of chromatographic systems but also influence the choice of methodology based on the nature of the mixture and desired purity and separation efficiency. By providing a scientific basis for predicting the behavior of compounds during chromatography, these models help optimize parameters and improve analytical outcomes.
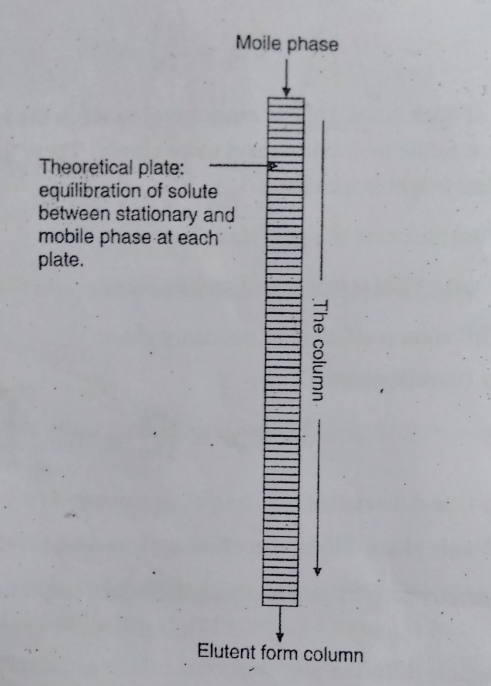
Rate Theory Explained
Definition and Fundamentals
Rate Theory, often termed kinetic theory, addresses the movement and separation of molecules in chromatography through kinetics. It fundamentally examines how molecules interact with the stationary phase and the mobile phase within a chromatographic system. The theory posits that the separation of compounds is significantly influenced by their movement rates, which depend on diffusion and flow dynamics.
Application in Chromatography
In practical chromatography, Rate Theory is instrumental in designing columns and selecting operational parameters that optimize the separation of substances. For example:
- Adjusting Flow Rate: Controlling the speed at which the mobile phase travels through the column affects how substances interact with the stationary phase.
- Temperature Management: Higher temperatures can increase the diffusion rates of molecules, influencing their travel through the column.
Key Concepts
Several key concepts underpin Rate Theory:
- Mass Transfer: This involves the transfer of analyte molecules between the stationary and mobile phases.
- Diffusion Coefficients: These are measures of how quickly molecules spread out due to random motion, affecting their path and speed in the column.
Plate Theory Overview
Basic Principles
Plate Theory simplifies the complex interactions in chromatography into a series of discrete steps or “theoretical plates.” Each plate represents an ideal equilibrium stage where the solute partitions between the mobile and stationary phases. This model helps in visualizing and calculating the separation efficiency and is pivotal in designing effective chromatographic processes.
Chromatographic Implications
Plate Theory is particularly useful in:
- Column Design: Engineers use the concept of theoretical plates to estimate the necessary column length and packing material for effective separation.
- Method Development: Analytical chemists apply plate numbers to gauge the efficiency of a chromatography system.
Core Elements
The core of Plate Theory lies in its ability to provide a straightforward metric—the number of theoretical plates. This number helps predict the resolution between two peaks in a chromatogram, indicating how well two components can be separated under set conditions.
Comparing Theories
Fundamental Differences
While Rate Theory focuses on the kinetics of molecules moving through the system, Plate Theory abstracts these movements into a series of equilibration stages. Rate Theory provides a more dynamic view of separation, whereas Plate Theory offers a static, segmented perspective.
Practical Applications in Analysis
Each theory guides different aspects of chromatographic method development:
- Rate Theory: Best for optimizing operational conditions like flow rate and temperature.
- Plate Theory: Useful for estimating column efficiency and the impact of different stationary phases.
Theoretical Implications
The choice between Rate Theory and Plate Theory often depends on the specific requirements of the analysis, such as the complexity of the mixture and the precision needed in the separation.
Impact on Chromatography
Effectiveness in Separation Processes
Both theories significantly impact the effectiveness of separation processes:
- Rate Theory: Enhances understanding of how to manipulate conditions to improve separation.
- Plate Theory: Provides benchmarks for expected performance and aids in troubleshooting and refining techniques.
Efficiency in Various Chromatographic Techniques
Different chromatographic techniques benefit from the insights provided by these theories:
- Gas Chromatography (GC): Plate Theory helps in understanding the resolution between volatile compounds.
- High-Performance Liquid Chromatography (HPLC): Rate Theory assists in managing the separation conditions for complex liquid mixtures.
Technical Comparisons
Mathematical Models in Rate Theory
Rate Theory uses mathematical models to describe the kinetics of solute migration through the chromatographic column. The primary equation in Rate Theory is the van Deemter equation, which integrates various factors like Eddy diffusion (A), longitudinal diffusion (B), and mass transfer (C) terms:
𝐻=𝐴+𝐵𝑢+𝐶𝑢H=A+uB+Cu
where 𝐻H represents the height equivalent to a theoretical plate (HETP), and 𝑢u is the linear velocity of the mobile phase. This equation helps predict the efficiency of separation under varying flow rates and can be adjusted to improve performance.
Mathematical Models in Plate Theory
In contrast, Plate Theory utilizes the concept of theoretical plates to model separation. The key equation here is the resolution equation:
𝑅=𝑁0.5×(𝑘′/(1+𝑘′))×(ΔΔ)4R=4N0.5×(k′/(1+k′))×(ΔΔ)
where 𝑅R is the resolution, 𝑁N is the number of theoretical plates, 𝑘′k′ is the capacity factor, and ΔΔΔΔ represents the selectivity factor between two peaks. This model emphasizes the importance of column efficiency as represented by the number of plates, aiming to optimize the column’s length and the conditions for separation.
Predictive Accuracy and Limitations
Both models serve crucial roles but come with inherent limitations:
- Rate Theory is praised for its dynamic representation of chromatographic processes but can become complex when predicting outcomes in highly interactive mixtures.
- Plate Theory, while simpler and often effective for standard separations, may not accurately predict the behavior of analytes in more complex or longer columns.
Case Studies
Real-world Application of Rate Theory
A notable application of Rate Theory is in the optimization of protein purification using HPLC. By adjusting the flow rate and analyzing the impact on protein peak broadening, researchers can significantly enhance the purity and yield of the protein.
Real-world Application of Plate Theory
In the pharmaceutical industry, Plate Theory has been applied to ensure the consistency and quality of drug products. By calculating the number of theoretical plates, technicians can routinely check the efficiency of the chromatography columns used in the quality control of raw materials and finished products.
Challenges and Limitations
Limitations of Rate Theory
Rate Theory’s limitations become evident when dealing with very large or very small molecules. Its predictive power decreases due to:
- Non-ideal diffusion behavior in large molecules like proteins.
- Overestimation of peak broadening at high flow rates, leading to less accurate predictions.
Limitations of Plate Theory
Plate Theory, while effective in routine analyses, struggles with:
- Non-linear separations where the interaction between the analyte and the stationary phase does not fit simple equilibrium models.
- Complex mixtures where multiple interactions occur, which the theory cannot effectively model.
Future Directions
Advances in Chromatographic Theories
The future of chromatographic theories lies in the integration of computational models and machine learning to enhance both Rate and Plate Theories. These advances aim to provide more accurate predictions across a wider range of conditions and mixtures.
Potential Modifications and Improvements
Potential improvements in chromatographic techniques might include:
- Hybrid models that combine the dynamic aspects of Rate Theory with the structural insights of Plate Theory.
- Automation in parameter optimization, using artificial intelligence to quickly determine optimal conditions for any given separation challenge.
Frequently Asked Questions
What is Rate Theory?
Rate Theory explains the separation of components in chromatography through the kinetics of molecular movement. It considers the effects of diffusion and the velocity of molecules moving through the stationary phase, providing insights into the efficiency of separation based on kinetic parameters.
How does Plate Theory work?
Plate Theory models the chromatography column as consisting of numerous theoretical plates. Each plate represents a zone where solute equilibration between the mobile and stationary phases occurs. This theory helps predict the resolution and effectiveness of separation by calculating the number of plates.
Why compare Rate and Plate Theories?
Comparing Rate and Plate Theories highlights their applicability and limitations in different chromatographic scenarios. Understanding these differences is crucial for selecting the appropriate model to achieve optimal separation results based on the specific characteristics of the sample and analytical requirements.
What impacts chromatographic efficiency?
Chromatographic efficiency is influenced by factors like the particle size of the stationary phase, the flow rate of the mobile phase, and the temperature of the column. Both Rate and Plate Theories provide frameworks to understand and optimize these parameters to enhance the resolution and speed of analysis.
Conclusion
The exploration of Rate Theory and Plate Theory within chromatography underscores the complexity and sophistication of this analytical technique. These theoretical models offer distinct yet complementary perspectives that enrich our understanding of the separation processes, enabling more precise and effective analytical practices.
As advancements in chromatographic technology continue, the interplay between these theories and practical applications will undoubtedly evolve. This ongoing development not only promises enhanced analytical capabilities but also fosters a deeper comprehension of the fundamental principles governing chromatographic separation. This knowledge is vital for scientists and researchers striving to achieve superior analytical outcomes in various fields of study.

