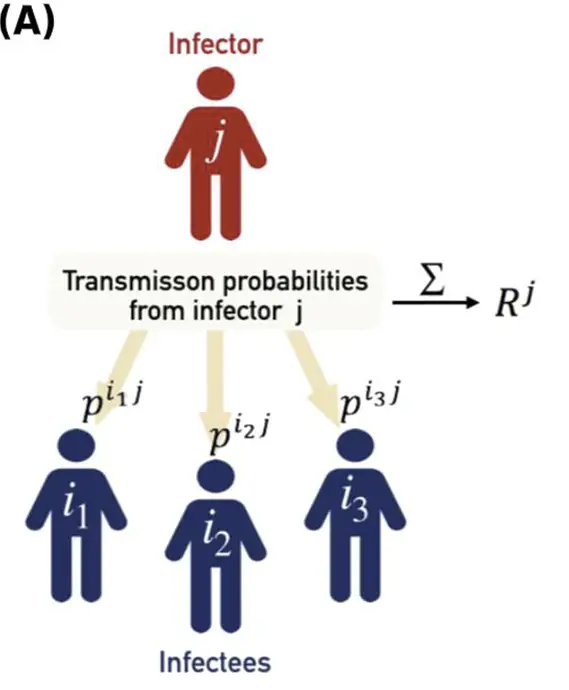
Reproduction numbers are fundamental concepts in epidemiology, playing a crucial role in understanding the spread of infectious diseases. These metrics, often referred to as π 0R0β (basic reproduction number) and π πReβ (effective reproduction number), help public health officials predict how quickly a disease can spread through a community. Accurate measurement of these numbers allows for effective planning and intervention, crucial in the fight against epidemics.
The basic reproduction number, π 0R0β, indicates the average number of people to whom a single infected individual will transmit the disease in a fully susceptible population. Conversely, the effective reproduction number, π πReβ, reflects the average number of secondary infections from a single case in a population where some individuals may no longer be susceptible, often due to immunity or public health interventions. The difference between these two values can significantly influence public health strategies and disease control measures.
While π 0R0β provides a snapshot of the diseaseβs potential to spread in the absence of any interventions or immunity, π πReβ offers a more dynamic and realistic picture by accounting for changes over time. Understanding these concepts is essential for developing strategies to contain outbreaks effectively and efficiently, enabling health systems to manage resources and prevent widespread transmission.
Basic Reproduction Number
Definition and Explanation
The basic reproduction number, commonly symbolized as π 0R0β (pronounced βR naughtβ), serves as a critical indicator in epidemiology to gauge the potential spread of an infectious disease within a completely susceptible population. It quantifies the average number of secondary infections that one infected individual is expected to produce in a setting where no other individuals are immune and no specific preventive measures are in place. A disease with an π 0R0β greater than 1 is expected to spread rapidly, whereas a value less than 1 indicates that the disease will likely diminish over time.
Factors Influencing the Basic Reproduction Number
Several factors can significantly alter the π 0R0β of a disease, including:
- Biological characteristics: The mode of transmission (airborne, droplet, vector-borne, etc.) and the infectious period of the pathogen.
- Behavioral patterns: Community behaviors such as hygiene practices, social gatherings, and travel.
- Environmental conditions: Climate factors that can affect the survival of the pathogen outside the host.
These elements intertwine to shape the basic reproductive number, making it a flexible figure rather than a static measure.
Role in Outbreak Assessment
Understanding π 0R0β is pivotal for public health officials to assess the potential severity of an outbreak and to strategize for effective containment. If π 0R0β is high, it suggests that aggressive interventions are necessary to prevent widespread disease transmission. This metric essentially helps in:
- Predicting the spread of disease
- Informing public health interventions
- Guiding policy decisions during the early stages of an outbreak
Effective Reproduction Number
Definition and Explanation
The effective reproduction number, or π πReβ, reflects how a disease is actually spreading at any point in time, considering the level of immunity and the effectiveness of interventions already in place. Unlike π 0R0β, which assumes a fully susceptible population, π πReβ accounts for the real-world scenarios where individuals may have developed immunity, through previous infection or vaccination, and where measures like social distancing or mask mandates are affecting transmission.
Differences from the Basic Number
π πReβ is dynamic, changing with the epidemiological environment and policy adjustments. Key differences between π 0R0β and π πReβ include:
- Susceptibility: π πReβ factors in the existing immunity in the population.
- Interventions: π πReβ is directly influenced by public health measures such as quarantines and vaccinations.
Understanding these distinctions is essential for accurately tracking and responding to an infectious disease outbreak as it evolves.
Impact of Interventions on Its Value
The effective reproduction number can provide insight into the success of public health interventions. A decrease in π πReβ to below 1 typically indicates that interventions are effective and that the outbreak is under control. Public health strategies can thus be tailored based on the current π πReβ value, allowing for more nuanced and effective management of disease spread.
Calculation Methods
Techniques for Estimating Basic Reproduction Number
Estimating π 0R0β involves various epidemiological models and statistical tools. Common methods include:
- Mathematical modeling: Using compartmental models in epidemiology, such as the SIR (susceptible-infected-recovered) model.
- Statistical analysis: Employing complex data sets to estimate how quickly a disease spreads without interventions.
Techniques for Estimating Effective Reproduction Number
Similarly, π πReβ is estimated using:
- Real-time modeling: Adjusting models to account for new data on case counts and the impact of interventions.
- Adaptive strategies: Updating estimates as new information about disease and population immunity becomes available.
Comparing Methodologies and Tools
Comparing these methodologies involves considering their applicability to different stages of an outbreak, the availability of data, and the specific characteristics of the disease being modeled. Itβs crucial to choose the right model and method based on the scenario at hand to ensure accuracy and effectiveness in estimating these crucial epidemiological parameters.
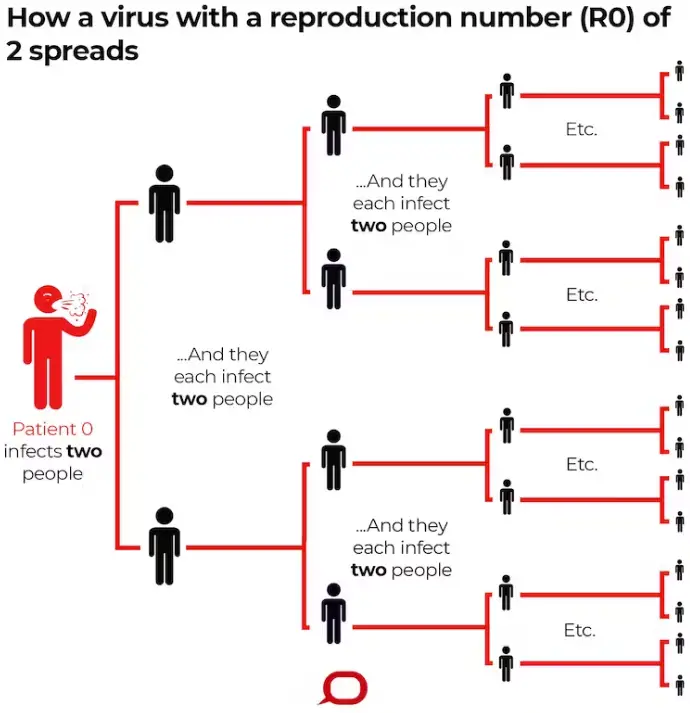
Case Studies
Historical Examples of Basic Reproduction Number
The concept of the basic reproduction number has been pivotal in studying past outbreaks and their control. A notable example is the 1918 influenza pandemic, often referred to as the Spanish Flu. Studies suggest that the π 0R0β for the 1918 pandemic was typically between 1.4 and 2.8, indicating a highly contagious virus. By comparing these historical values with more recent influenza outbreaks, epidemiologists can gauge differences in virus transmissibility and the effectiveness of modern public health interventions.
Another historical case is the eradication of smallpox. The π 0R0β of smallpox was estimated to be around 5 to 7 before the introduction of widespread vaccination. The global vaccination campaign, which effectively brought the π 0R0β down to less than one, showcases how understanding and manipulating this number can lead to the containment and even eradication of a disease.
Real-world Application of Effective Reproduction Number
During the COVID-19 pandemic, the effective reproduction number π πReβ has been used extensively to monitor and manage the outbreak. Different countries have reported varying π πReβ values in response to their specific public health strategies, such as lockdowns, mask mandates, and social distancing measures. For instance, after initial lockdown measures, Italy and Spain saw their π πReβ values decrease significantly from well above 1 to below this threshold, demonstrating the effectiveness of stringent public health interventions.
Analysis of Intervention Outcomes
Analyzing the outcomes of interventions using π πReβ offers tangible insights into their efficacy. For example, during the Ebola outbreak in West Africa, the implementation of community care centers and safer burial practices were monitored by observing changes in π πReβ. As interventions took place, a marked reduction in π πReβ was noted, which correlated with a decrease in cases and, ultimately, the containment of the outbreak.
Implications in Public Health
Decision-making Based on Reproduction Numbers
Reproduction numbers are crucial in guiding public health decisions. For example, when π 0R0β or π πReβ is high, governments may decide to close schools, restrict travel, or implement lockdowns to reduce transmission. Conversely, a low π πReβ might encourage the lifting of such restrictions. This data-driven approach ensures that interventions are timely and proportionate to the threat level of the disease.
Forecasting and Containment Strategies
Effective forecasting and containment strategies are often based on models that incorporate π 0R0β and π πReβ. These models help predict disease spread patterns, enabling proactive measures. For instance, predictive modeling was used during the H1N1 influenza pandemic to allocate resources like vaccines and antiviral drugs effectively before the winter season, which is typically the peak time for influenza.
Challenges in Accurate Estimation
Despite the utility of π 0R0β and π πReβ, several challenges hinder their accurate estimation:
- Data Quality: Incomplete or inaccurate infection case reports can skew reproduction number estimates.
- Population Diversity: Variations in susceptibility and behavior across different demographics can complicate the calculations.
- Change in Policy and Compliance: Fluctuations in public health policies and public compliance over time can affect the accuracy of π πReβ.
These factors necessitate continuous data updates and model adjustments to ensure reliable predictions and effective public health responses.
FAQs
What is π 0R0β?
The basic reproduction number, or π 0R0β, is a measure used to describe the intensity of an infectious disease outbreak. It represents the average number of people that a single infectious individual will infect if no other individuals in the community are immune or no preventive measures are taken.
How is π πReβ different from π 0R0β?
While π 0R0β assumes no control measures or previously acquired immunity within a population, the effective reproduction number, π πReβ, takes these factors into account. π πReβ changes with the implementation of public health strategies and the development of immunity, reflecting the current potential for disease spread.
Why do π 0R0β and π πReβ matter?
These metrics are crucial for public health planning and response. They help determine the level of intervention required to control an outbreak and are fundamental in forecasting future disease spread, guiding strategies for vaccination, social distancing, and other interventions.
Can π 0R0β and π πReβ change over time?
Yes, while π 0R0β is generally considered a constant value for a given disease, π πReβ can vary as population immunity develops and as public health measures are introduced or relaxed. This makes π πReβ a more flexible and frequently updated metric during an outbreak.
Conclusion
Understanding the distinction between the basic and effective reproduction numbers is more than academic; itβs a critical component of disease prevention and control. These metrics not only guide immediate public health responses but also influence long-term strategies in managing infectious diseases. As such, accurate estimation and thorough understanding of π 0R0β and π πReβ are indispensable in the realm of epidemiology.
With ongoing research and data collection, our grasp of these parameters will continue to refine, leading to more precise and effective interventions. Ultimately, the knowledge of π 0R0β and π πReβ empowers public health professionals to anticipate disease trends and craft strategies that can significantly mitigate the impact of infectious diseases on society.