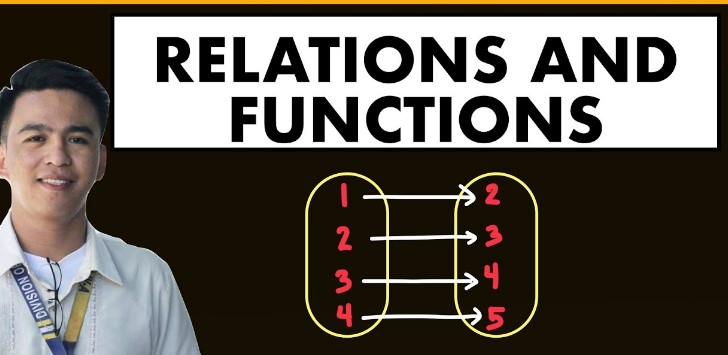
Mathematical concepts are foundational to understanding the world around us, serving as the backbone of disciplines ranging from engineering to economics. At the heart of these concepts lie functions and relations, two crucial constructs that govern how different quantities relate to each other. While often mentioned in the same breath, their differences are significant and foundational to their application in various mathematical contexts.
The difference between a function and a relation lies primarily in their definitions and how they associate elements from one set to another. A relation is any association between sets of information. In contrast, a function is a specific type of relation where each input is related to exactly one output. This fundamental distinction underpins their application in mathematics and beyond, affecting how problems are approached and solved.
Functions and relations play pivotal roles in not just mathematics but also in real-life scenarios and other fields such as computer science and physics. Understanding their differences is not just an academic exercise but a practical necessity for problem-solving and innovation. Their application ranges from determining the relationship between variables in a scientific experiment to optimizing algorithms in computer programming.
Core Definitions
What is a Relation?
Definition and Explanation
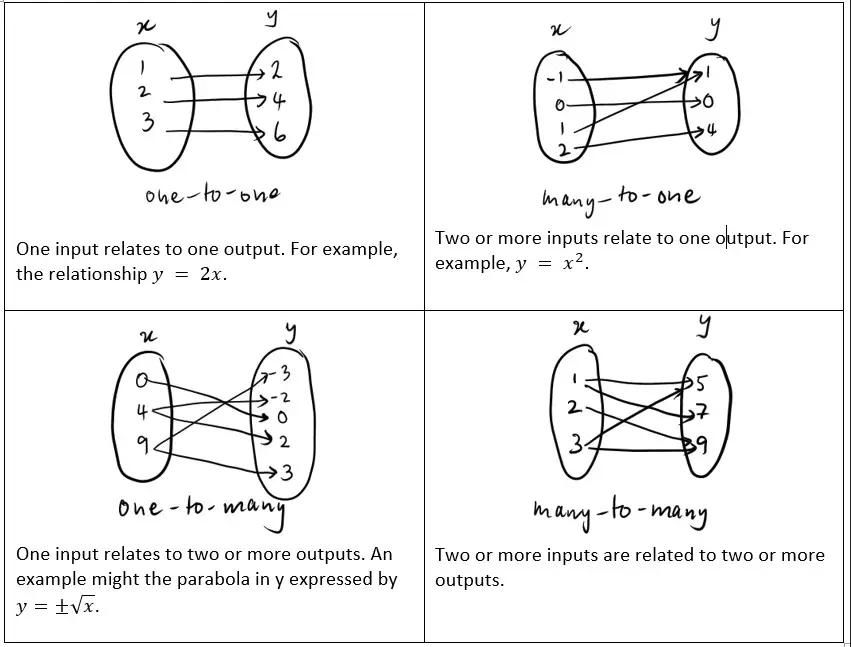
A relation represents a connection between two sets of information. Specifically, it defines how elements from one set, known as the domain, are associated with elements from another set, referred to as the codomain. This association does not necessitate a one-to-one correspondence; a single element from the domain can be linked to multiple elements in the codomain.
Types of Relations
Relations are categorized based on how they associate elements between sets. The primary types include:
- Reflexive: Every element is related to itself.
- Symmetric: If an element A is related to B, then B is also related to A.
- Transitive: If A is related to B, and B is related to C, then A is related to C.
- Equivalence: Relations that are reflexive, symmetric, and transitive.
- Functional: Each element of the domain is associated with exactly one element of the codomain.
Examples in Mathematics and Real-Life
In mathematics, a relation might describe the link between students and their chosen subjects, where a student (domain) can enroll in multiple subjects (codomain). In real life, a relation could describe the association between customers and their purchased items in a store.
What is a Function?
Definition and Clarification
A function is a specific type of relation where each input (an element of the domain) is associated with exactly one output (an element of the codomain). This unique characteristic ensures a predictable relationship between inputs and outputs, making functions fundamental in mathematical calculations and applications.
Functions vs. Other Mathematical Expressions
Functions distinguish themselves from other mathematical expressions by their one-to-one correspondence between the domain and codomain. Unlike general relations, functions provide a clear and direct mapping, ensuring that for every input, there is a single, well-defined output.
Real-Life Examples of Functions
Functions appear in various real-life scenarios, such as:
- Speed and Time: The function linking time to the distance traveled by a car, where each moment in time corresponds to one specific location.
- Bank Transactions: A function that describes the relationship between the number of transactions and the account balance.
Key Differences
Unique Characteristics
The core distinction between functions and relations lies in their handling of domain and codomain elements. While a relation can associate a single domain element with multiple codomain elements, a function restricts this to a one-to-one mapping. This fundamental difference underlines the precision and predictability of functions.
Comparison of Function and Relation Characteristics
While all functions are relations due to their associative nature, not all relations qualify as functions. This subset relationship highlights the stricter criteria functions must meet, emphasizing their role in providing consistent, unambiguous results.
How Functions are a Subset of Relations
Functions are considered a subset of relations because they adhere to a more stringent condition: each domain element corresponds to one and only one codomain element. This criterion is not required for general relations, making functions a specialized form of relation.
Mapping and Pairs
Explanation of Domain, Codomain, and Range
- Domain: The set of all possible inputs.
- Codomain: The set of all potential outputs, as defined by the relation or function.
- Range: The actual set of outputs that are achieved from the domain through the relation or function.
Functions and relations approach these concepts with notable differences. Functions ensure a unique output for each input, thereby defining a precise range within the codomain. Relations, being more general, may not utilize the entire codomain, as multiple outputs can be associated with a single input.
Visualization
Graphical Representation of Functions and Relations
Graphs offer a visual way to distinguish between functions and relations. By plotting the domain against the codomain, one can visually assess the nature of the association.
- Functions display a clear one-to-one mapping, where each x-value (input) corresponds to a single y-value (output).
- Relations might show that a single x-value links to multiple y-values, indicating the broader associative capabilities of relations.

Functions and Relations in Use
Mathematical Applications
Functions and Relations in Calculus
Calculus, the study of change, relies heavily on the concepts of functions and relations to describe the behavior of variables. Functions play a crucial role in both differential and integral calculus, where the focus is on the rates at which quantities change and the accumulation of quantities, respectively.
- Differential Calculus: Functions allow us to find the derivative, which represents the rate of change. For example, in physics, the speed of an object can be determined by deriving its position function with respect to time.
- Integral Calculus: Functions are integral (no pun intended) in finding the area under curves, among other applications. This helps in calculating quantities like distance traveled when given a speed function.
Role in Algebraic Structures
In algebra, both functions and relations are foundational in understanding how different algebraic structures interact. For example:
- Functions can map elements from one group to another, preserving structure and operations, which is key in the study of group theory.
- Relations, such as equivalence relations, help in partitioning sets into equivalent classes, a fundamental concept in set theory.
Practical Examples
Functions and Relations in Computer Science
In computer science, functions and relations are everywhere, from the basics of algorithms to the complexities of databases.
- Algorithms: Functions are used to encapsulate a sequence of instructions that perform a specific task. For example, a sorting function takes a list of elements as input and returns them in a certain order.
- Databases: Relations are the basis of relational databases, where data is stored in tables that relate to each other through keys.
Everyday Scenarios Where the Difference Matters
Understanding the difference between functions and relations can be crucial in daily decision-making processes. For example:
- Navigation Systems: Functions determine the best route from point A to point B, ensuring each starting point (A) has a single optimal endpoint (B).
- Healthcare: Monitoring a patient’s health can be seen as a function where each patient’s data (input) corresponds to specific health outcomes (output).
Advanced Concepts
Inverse Relations and Functions
Understanding Inverse Processes
The concept of inverse functions and relations is essential in undoing the effect of the original function or relation. For an inverse function to exist, the function must be bijective, meaning it’s both injective (one-to-one) and surjective (onto).
- Real-life Example: If you have a function that converts temperatures from Celsius to Fahrenheit, the inverse function would convert Fahrenheit back to Celsius.
Conditions for Inverses in Functions and Relations
For a function to have an inverse:
- It must be bijective.
- Each output should be linked to one and only one input.
- Graphically, if a function passes the horizontal line test (every horizontal line intersects the graph at most once), it has an inverse.
Complex Relations and Functions
Multi-variable Functions
Multi-variable functions, which involve more than one input, expand the complexity and applicability of functions in modeling real-world scenarios. For example:
- Economic Models: A function could model how different factors (inputs) like interest rates and investment affect economic growth (output).
Complex Relations in Higher Mathematics
In higher mathematics, complex relations explore relationships that are not functions because they don’t meet the criteria of pairing each input with a single output. These relations can model more complex systems, such as:
- Social Networks: The connections between people (where one person can be connected to multiple others) represent a non-functional relation but are crucial for understanding social dynamics.
Frequently Asked Questions
Can a relation be a function?
Yes, a relation can be a function if it adheres to a specific criterion: every input or element of the domain must be associated with exactly one output or element of the codomain. This unique characteristic distinguishes functions from broader relations, where an input can have multiple outputs.
How do graphs help differentiate between functions and relations?
Graphs visually represent the relationship between inputs and outputs. For a graph to represent a function, any vertical line drawn through the graph must intersect it at no more than one point. This “vertical line test” helps differentiate functions from relations, which might have multiple intersections with a vertical line, indicating multiple outputs for a single input.
Why is understanding the difference between functions and relations important?
Understanding the difference is crucial for solving mathematical problems accurately and applying mathematical concepts in real-life situations. Functions, with their unique one-to-one relationship between inputs and outputs, offer predictability and specific patterns that are essential in fields like engineering, computer science, and physics. Relations, being more general, are foundational in understanding complex associations between sets.
Conclusion
Recognizing the difference between functions and relations is more than an academic pursuit; it’s a cornerstone of logical reasoning and problem-solving in various fields. This distinction allows us to approach problems with the right tools, ensuring clarity, accuracy, and innovation in solutions. As we navigate through complex mathematical landscapes, the understanding of these foundational concepts enriches our comprehension and application of mathematics in real-world scenarios.
The journey through the realms of functions and relations illuminates the beauty and precision of mathematics. It underscores the importance of clear definitions and the power of mathematics to model the complexity of the world around us. As we continue to explore and apply these concepts, our ability to solve problems, big and small, becomes ever more refined and effective.