Analytical chemistry plays a crucial role in understanding the composition of chemical substances and their reactions. Among its various methodologies, Job’s Method and Mole Ratio Method stand out due to their unique approaches in determining the stoichiometry of chemical complexes. These methods are not just academic exercises but are essential tools in research and industry for the precise quantification and analysis of compounds.
The difference between Job’s Method and Mole Ratio Method lies primarily in their procedural approach and the type of data they provide. Job’s Method, also known as the method of continuous variations, identifies the stoichiometry of a complex by varying the proportions of reactants until the maximum amount of product is formed. On the other hand, the Mole Ratio Method determines the stoichiometry by measuring the reaction’s completeness at different molar ratios of the reactants, identifying the ratio that leads to the highest yield of product.
Both methods are invaluable in the realm of analytical chemistry, each with its advantages and specific applications. Job’s Method is particularly useful in identifying the precise stoichiometry of a complex, while the Mole Ratio Method excels in confirming the most efficient molar ratios for reactions. Understanding the distinctions between these methods is vital for chemists and researchers who strive to optimize reactions and understand the underlying principles of their work.
Job’s Method Overview
Definition and Basics
Job’s Method, often known as the method of continuous variations, is a classical analytical technique used to determine the stoichiometry of complexes in solution. At its core, this method involves varying the proportions of two reactants while keeping the total amount constant to find the mixture’s composition that reacts completely without any excess of either reactant. This particular composition reflects the stoichiometric ratio of the components in the complex.
Historical Background
Developed in the early 20th century, Job’s Method has roots in the foundational work of chemists seeking to understand the quantitative aspects of chemical reactions. The method is named after the French chemist, Job, who popularized this approach. It emerged from the necessity to accurately determine the composition of complex chemical entities, a task that remains vital in both academic and industrial laboratories.
Key Applications
Job’s Method is widely utilized in:
- Synthesis research: Determining the optimal ratios for synthesizing complex compounds.
- Pharmaceuticals: Establishing the precise composition of drug compounds.
- Environmental chemistry: Analyzing pollutants and their interaction with natural compounds.
Mole Ratio Method Overview
Definition and Essentials
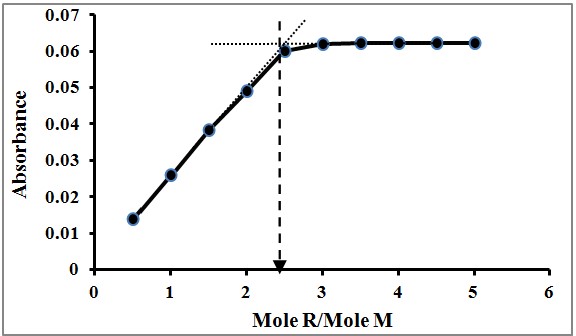
The Mole Ratio Method is another pivotal technique in analytical chemistry, designed to find the optimal ratio of reactants that produces the maximum amount of a desired product. This method involves conducting a series of reactions with varying mole ratios of the reactants and observing the point at which the highest yield of product is achieved. This optimal ratio is indicative of the stoichiometry of the reaction.
Historical Perspective
Like Job’s Method, the Mole Ratio Method has its origins in the early pursuits of chemistry to quantify reaction components. Over time, it has been refined and adapted to suit a wide range of chemical analyses, benefitting from advancements in measurement and detection technologies.
Main Applications
The Mole Ratio Method finds its use in:
- Catalysis: Optimizing the ratio of catalyst to reactants in industrial processes.
- Material science: Developing new materials with desired properties.
- Biochemistry: Studying enzyme-substrate interactions.
Comparative Analysis
Conceptual Differences
Fundamental Principles
While both methods aim to elucidate stoichiometry, they differ in approach. Job’s Method focuses on identifying the exact stoichiometric ratio in a complex, whereas the Mole Ratio Method is about finding the most effective reactant proportions for achieving the highest yield.
Procedure Variations
- Job’s Method: Involves systematic variation of reactant proportions in a single solution.
- Mole Ratio Method: Conducts separate reactions for each set of reactant ratios.
Technical Aspects
Required Equipment and Materials
- Common Requirements: Both methods require standard laboratory equipment like beakers, pipettes, and analytical balances.
- Specific Needs: The Mole Ratio Method might additionally require separate reaction vessels for each ratio tested.
Steps Involved in Each Method
Job’s Method
- Prepare a series of solutions with varying ratios of two reactants.
- Measure the response (e.g., absorbance, precipitation) for each mixture.
- Analyze the data to find the ratio with the strongest response, indicating the stoichiometric ratio.
Mole Ratio Method
- Set up separate reactions for each mole ratio of interest.
- Measure the yield or another indicator of reaction completeness for each.
- Determine which ratio results in the highest yield, signifying the optimal stoichiometry.
Accuracy and Precision
Comparison of Accuracy Levels
Both methods can achieve high accuracy when properly executed. However, the precision of Job’s Method in determining stoichiometry might edge out the Mole Ratio Method, which excels in practical applications where yield is the focus.
Factors Affecting Precision
- Experimental Conditions: Temperature, solvent, and purity can influence both methods.
- Measurement Techniques: The precision of the measuring instruments directly impacts the results.
Suitability and Limitations
Ideal Scenarios for Each Method
- Job’s Method: Best when exact stoichiometry is needed.
- Mole Ratio Method: Preferred for optimizing reaction conditions.
Known Limitations and Challenges
- Job’s Method: Can be tedious and requires careful measurement.
- Mole Ratio Method: Might not provide the exact stoichiometry but is effective in practical yield optimization.
Frequently Asked Questions
What is Job’s Method?
Job’s Method, rooted in the principle of continuous variations, is a quantitative technique in chemistry used to deduce the stoichiometry of a chemical complex. By systematically altering the ratios of two reactants while keeping their total amount constant, researchers can pinpoint the ratio that yields the maximum amount of product, thereby determining the stoichiometric relationship within the complex.
How does the Mole Ratio Method work?
The Mole Ratio Method involves varying the molar ratios of reactants in a series of reactions to find the ratio that leads to the highest yield of a desired product. This method is crucial for determining the most efficient stoichiometry for a reaction, aiding in the optimization of chemical processes and the understanding of reaction mechanisms.
Why choose Job’s Method over the Mole Ratio Method?
Choosing between Job’s Method and the Mole Ratio Method depends on the specific needs of the experiment. Job’s Method is preferred when the primary goal is to accurately determine the stoichiometry of a complex compound. In contrast, the Mole Ratio Method is selected for its ability to identify the optimal reactant ratios for achieving the highest yield in a chemical reaction.
Can these methods be used in all chemical reactions?
While Job’s Method and the Mole Ratio Method are versatile, their applicability may vary depending on the type of reaction and the reactants involved. Factors such as reaction speed, complexity, and the physical state of the reactants can influence the effectiveness of each method. It is essential to evaluate the specific requirements and limitations of a reaction when choosing the most appropriate method.
Conclusion
Job’s Method and the Mole Ratio Method are foundational techniques in analytical chemistry, each offering unique insights into the stoichiometry of chemical reactions. Their differences lie not only in their procedural aspects but also in their applications and the specific types of data they provide. Understanding these methods enhances our ability to conduct precise and efficient chemical analyses, contributing to advancements in research and industrial practices.
The choice between Job’s Method and the Mole Ratio Method should be guided by the objectives of the experiment, whether it is the determination of exact stoichiometry or the optimization of reactant ratios for maximum product yield. Both methods play indispensable roles in the broader field of chemistry, underlining the importance of methodological diversity in uncovering the complexities of chemical reactions.

