Mathematical concepts are the building blocks of logical reasoning and problem-solving skills. Among these, the concepts of relations and functions stand out for their fundamental role in various branches of mathematics and their applications in real-world scenarios. Understanding these concepts is crucial for students and professionals alike, as they form the basis for more complex mathematical theories and calculations.
The difference between a relation and a function lies in their definition and application: a relation is a set of ordered pairs, while a function is a special type of relation where each input is related to exactly one output. This distinction is key in mathematics, as it dictates how each concept is used in equations, graphs, and problem-solving.
Relations and functions each play unique roles in mathematics, with their own sets of rules, representations, and applications. While relations can model a broad range of scenarios with no restrictions on the number of outputs for a given input, functions are more specific, ensuring a single output for each input, which is fundamental for predicting outcomes in scientific and mathematical models.

Basic Concepts
Relations Defined
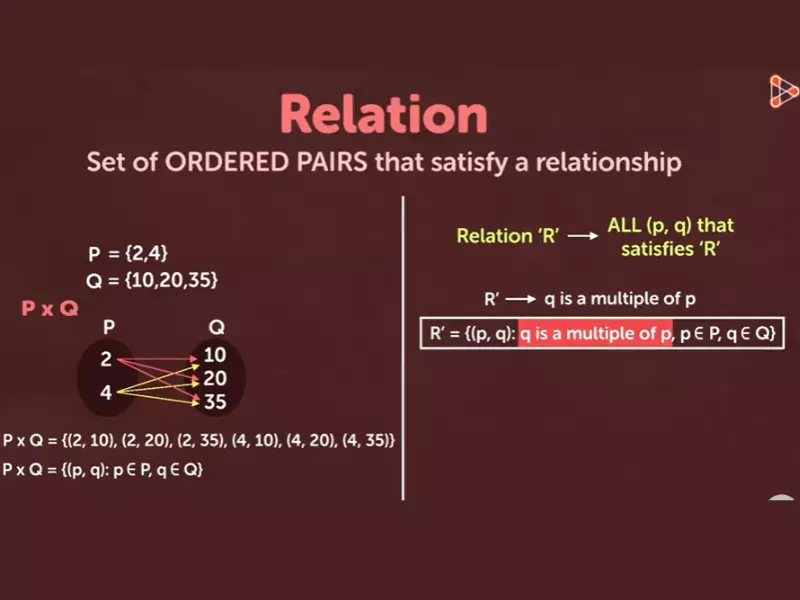
In mathematics, relations are ways to connect elements from two sets by pairing them together. Imagine you have two sets of numbers or objects. A relation between these sets pairs elements from the first set with elements from the second set. These pairings can be arbitrary and aren’t limited by any specific rule, other than the rule defining the relation itself.
Examples of Relations
- Friendship among people: Consider two sets where one includes people and the other includes their hobbies. A relation could pair each person with their favorite hobby.
- City to Country: Here, one set is cities, and the other is countries. The relation pairs each city with its country.
Functions Explained
Definition of a Function
A function is a specific type of relation with a unique requirement: each element from the first set (often called the domain) is paired with exactly one element from the second set (the range). This ensures that for every input, there is only one possible output.
Key Characteristics of Functions
Functions have three key characteristics:
- Uniqueness: For every input, there’s a single, unique output.
- Dependency: The output depends entirely on the input.
- Rule-based: A specific rule determines the output for each input.
Examples of Functions
- Square Function: Maps each real number to its square.
- Temperature Conversion: Converts temperatures from Celsius to Fahrenheit.
Core Differences
Unique Outputs
The requirement for unique outputs in functions distinguishes them significantly from general relations. While a relation can have multiple outputs for a single input, a function strictly adheres to a one-to-one rule.
Graphical Representation
Graphically, functions and relations can be plotted on a coordinate plane, but with a key difference.
- Functions: Can pass the vertical line test, meaning a vertical line will intersect the graph at most once.
- Relations: Might intersect a vertical line more than once if they are not functions.
Visual Examples
Consider plotting a simple linear function vs. a relation that pairs one input with multiple outputs. The function’s graph is a straight line, while the relation’s graph could have multiple lines or curves emanating from a single x-coordinate.
Mathematical Representation
In equations, functions are often represented with a specific notation, like �(�)f(x), indicating that �f is a function of �x. Relations, however, might not adhere to this format and can be represented as a set of ordered pairs without the implication of a function’s restrictions.
Notation Differences
- Function: �=�(�)=2�+3y=f(x)=2x+3
- Relation: {(�,�)∣�=2�+3,�=�2}{(x,y)∣y=2x+3,y=x2}
Specific Types
Types of Relations
Relations can be categorized into several types based on certain properties:
- Reflexive: Every element is related to itself.
- Symmetric: If �a is related to �b, then �b is related to �a.
- Transitive: If �a is related to �b and �b is related to �c, then �a is related to �c.
Examples and Non-examples
Reflexive Example: A person is as tall as themselves.
Non-example for Symmetric: Just because a person �A is the parent of person �B, doesn’t mean �B is the parent of �A.
Types of Functions
Functions can also be classified based on their equations and the shape of their graphs:
- Linear Functions: Graphs are straight lines.
- Quadratic Functions: Graphs are parabolas.
- Polynomial Functions: Include terms with variables raised to whole number powers.
Characteristics and Graphical Examples
- Linear Function: �(�)=��+�f(x)=mx+b produces a straight line.
- Quadratic Function: �(�)=��2+��+�f(x)=ax2+bx+c produces a parabola.
- Polynomial Function: �(�)=�3−4�f(x)=x3−4x shows curves that may change direction based on the power of �x.
By understanding these foundational concepts, readers gain insight into the intricate dance between relations and functions, two pillars of mathematical logic that illuminate the pathways of reasoning and problem-solving across numerous applications, from the theoretical to the practical realms.
In the sections to follow, we will delve deeper into the practical applications of these concepts, exploring how they manifest in real life and advanced mathematics, and addressing common confusions to ensure a robust comprehension of these fundamental mathematical ideas.
Practical Applications
In Real Life
Functions and relations find their utility in numerous real-world scenarios, making abstract mathematical concepts tangible and significantly impacting our daily lives and decision-making processes.
Applications of Functions and Relations
- Economics: Functions model the relationship between supply and demand, helping economists predict market trends and make policy decisions. A simple supply function can predict how changes in price impact the quantity supplied.
- Healthcare: Growth rates of bacteria or virus spread can be modeled using exponential functions, aiding in understanding and controlling outbreaks.
- Engineering: Relations and functions are used to design systems and structures, ensuring they work efficiently under various conditions.
Impact on Problem-Solving and Decision-Making
- Optimization: Functions help in optimizing resources, be it minimizing costs or maximizing efficiency in production processes.
- Predictive Analysis: By understanding the functional relationship between variables, businesses can forecast future outcomes, aiding in strategic planning.
- Data Analysis: Relations are used in database queries to fetch information that matches certain criteria, enhancing data retrieval and analysis.
In Advanced Mathematics
The concepts of functions and relations are not just foundational but are pivotal in higher mathematics, driving the development of theories and solutions across disciplines.
Role in Calculus, Algebra, and Other Fields
- Calculus: Functions are the heart of calculus, with concepts like limits, derivatives, and integrals relying on them to analyze changes.
- Algebra: From solving equations to exploring polynomial functions, algebra employs these concepts to establish relationships between variables.
- Linear Algebra: Functions describe transformations, and relations help understand vector spaces and matrices.
Importance for Further Mathematical Study
The mastery of functions and relations opens doors to advanced fields such as topology, complex analysis, and differential equations, where these concepts are further abstracted and applied.
Common Confusions
When Relations Become Functions
A crucial understanding in mathematics is identifying when a relation also qualifies as a function. The key lies in the uniqueness of outputs for each input within the domain.
Conditions under which a Relation Can Also be Considered a Function
- Every element in the domain must be paired with exactly one element in the range.
- If plotted on a graph, the relation must pass the vertical line test.
Visual and Theoretical Explanation
Consider a simple graph depicting a circle. As a relation, it pairs some x-values with multiple y-values. However, if we restrict our view to a semicircle (either top or bottom), it suddenly meets the criteria of a function—every x-value corresponds to a single y-value.
Misidentification Pitfalls
The subtle differences between functions and relations often lead to misidentification, impacting the understanding and application of these concepts.
Common Mistakes in Identifying Functions and Relations
- Assuming all relations are functions because they see pairs of numbers.
- Forgetting to apply the vertical line test to graphical representations.
- Confusing the terms “domain” and “range” can lead to incorrect conclusions about the nature of a mathematical concept.
Tips to Avoid Confusion
- Always Apply the Vertical Line Test: This simple graphical check can clarify whether you’re dealing with a function.
- Check Each Pairing Individually: Ensure each input has a single output.
- Review Definitions Regularly: Keeping the definitions of functions and relations at the forefront can help differentiate between them more effectively.
Understanding these distinctions and applications of functions and relations not only enhances mathematical literacy but also empowers individuals to apply these concepts in various scientific, engineering, and economic contexts. As we navigate through the complexities of the world, the ability to model, predict, and optimize using mathematics becomes a pivotal skill, rooted in a deep understanding of these foundational concepts.
In advanced mathematics, the journey continues as these concepts form the basis for more complex theories and applications, from the smooth curves of calculus to the abstract spaces of linear algebra. The exploration of functions and relations is a testament to the beauty and power of mathematics to describe the universe in its language.
As we conclude, remember that the journey through mathematics is one of discovery and application. The concepts of functions and relations are not just abstract notions but tools that shape our understanding of the world and empower us to make informed decisions, solve complex problems, and appreciate the intricate patterns that govern the natural and man-made worlds.
By demystifying common confusions and exploring the practical and theoretical sides of these concepts, we equip ourselves with the knowledge to advance further into the realms of mathematics and its applications. This journey through functions and relations is but a stepping stone to the vast and fascinating world of mathematical exploration and application, illuminating paths to innovation and understanding in countless fields.
FAQs
What is a Function in Mathematics?
A function in mathematics is a relation that uniquely associates each element of a given set with exactly one element of another set. Functions are fundamental in mapping scenarios where each input corresponds to one and only one output, making them essential for equations and models that require predictable results.
How is a Relation Different from a Function?
The main difference between a relation and a function is that a relation can associate a single input with multiple outputs, while a function restricts each input to a single output. This distinction is crucial for understanding how different mathematical models interpret and predict relationships between variables.
Can a Relation Be a Function?
Yes, a relation can be a function if it satisfies the condition of having each input related to exactly one output. Not all relations meet this criterion, making it essential to evaluate the specific characteristics of a relation to determine if it can also be considered a function.
Why are Functions Important in Mathematics?
Functions are important in mathematics because they provide a systematic way to describe how variables interact with each other. They allow for the creation of models that can predict outcomes, making them indispensable in fields ranging from physics and engineering to economics and beyond.
Conclusion
Understanding the difference between relations and functions is more than an academic exercise; it’s a foundational aspect of mathematical literacy that impacts various scientific and analytical fields. These concepts help shape our approach to problem-solving and enable us to model and predict outcomes in a structured manner.
Recognizing the unique characteristics and applications of relations and functions enriches our mathematical understanding and enhances our ability to apply these concepts in real-world scenarios. As we continue to explore the vast landscape of mathematics, appreciating these distinctions becomes a key step in our journey toward deeper knowledge and innovation.
