The probability density function (pdf) and cumulative density function (cdf) are two ways of representing a probability distribution. In this blog, we will discuss the underlying relationship between the pdf and cdf and how they are used to represent data. We will also explore the practical applications of these two functions and how they can be used to analyze data and draw conclusions.
We will also explore the practical applications of these two functions and how they can be used to analyze data and draw conclusions.
Theoretical overview of pdf and cdf
The relation between probability density functions (PDF) and cumulative distribution functions (CDF) is one of the fundamental concepts in probability theory. A PDF describes the probability of the occurrence of a certain event or outcome, while a CDF is a cumulative measure of the probability of the event occurring up to a certain point.
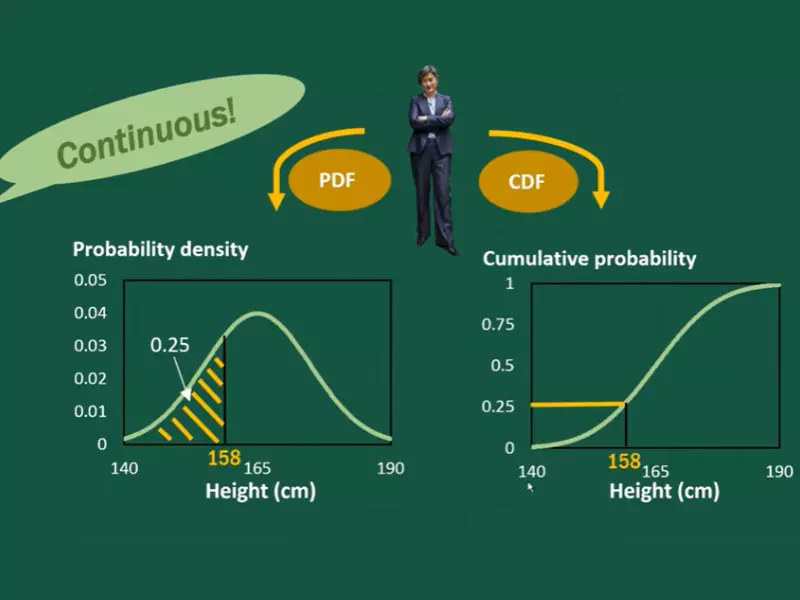
In other words, a PDF provides a snapshot of the probability of an event at any given point in time, while a CDF gives a cumulative view of the probability of the event occurring at any given point or over a period of time.
In other words, a PDF provides a snapshot of the probability of an event at any given point in time, while a CDF gives a cumulative view of the probability of the event occurring at any given point or over a period of time. In essence, the PDF and CDF together provide a complete picture of the probability of an event occurring.
Benefits of understanding the relationship between pdf and cdf
The relationship between probability density function (pdf) and cumulative distribution function (cdf) is a fascinating one. Understanding this relationship can provide insights into the probability of an event occurring, the expected value of a function, and the likelihood of a certain outcome.
In addition, it can help us identify patterns in data, identify outliers, and make decisions based on probability. With this knowledge, we can make more informed decisions and better understand the probability of a certain outcome. By understanding the relationship between pdf and cdf, we can maximize our chances of success in any situation.
How to calculate pdf and cdf
Understanding the relationship between probability density functions (pdfs) and cumulative distribution functions (cdfs) is essential for interpreting data correctly. A pdf is a mathematical function that describes the likelihood of a certain event occurring, while a cdf is a cumulative measure of the probability of that event occurring.
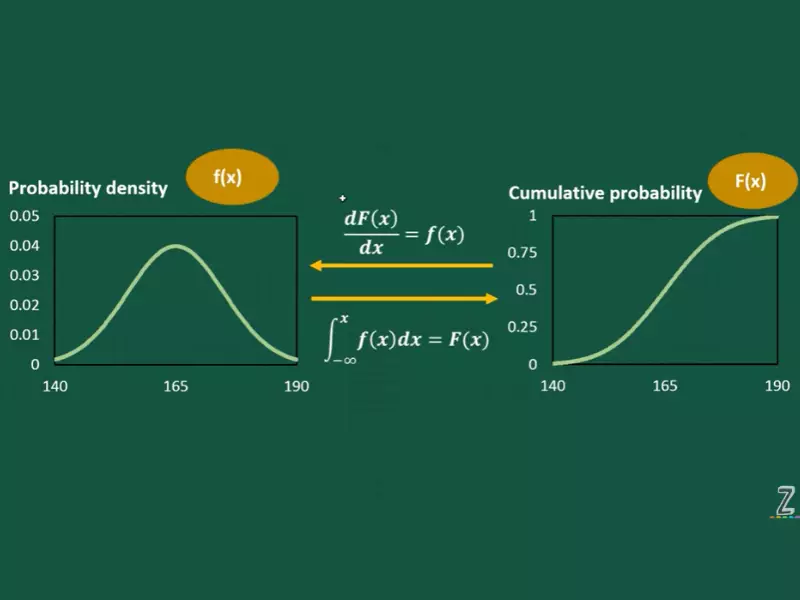
The cdf is derived from the pdf by integrating the probability density function over the entire range of possible values. This integration process allows us to calculate the probability of an event occurring at any point within the range of possible values. In other words, the cdf tells us the probability that a certain event will occur up to and including a certain point, while the pdf tells us the likelihood of a certain event happening at any point.
By understanding the relationship between pdfs and cdfs, we can use both to gain insight into our data.
Common use cases of pdf and cdf
When talking about probability distribution functions, the two most commonly discussed are the probability density function (pdf) and the cumulative distribution function (cdf). Both of these functions are related to each other, and understanding how they are linked can be extremely helpful for data analysis. The pdf gives us insight into the probability of a given value, while the cdf gives us insight into the cumulative probability of a given value.
This relationship can be used to determine the probability of a given outcome, as well as other related probabilities. Understanding the relation between pdf and cdf can be beneficial in a variety of contexts, such as predicting future events or examining the relationships between different variables.
Visualization of pdf and cdf
The relationship between a probability density function (pdf) and a cumulative distribution function (cdf) is an important concept in statistics. A pdf is a representation of the probability of an event occurring at any given point, while a cdf is a representation of the cumulative probability of an event occurring up to a certain point.
This relationship can be visualized in a graph, with the pdf on the x-axis and the cdf on the y-axis. As the x-axis increases, the y-axis increases, showing the cumulative probability of the event.
This relationship between the pdf and cdf is a powerful tool for understanding the probability of events and can be used to make predictions based on past data.
Final Touch
In conclusion, the relationship between the probability density function (PDF) and the cumulative distribution function (CDF) can be summarized as follows: the PDF is used to describe the probability of observing a given value or event, while the CDF is used to describe the cumulative probability of observing a given value or event. The PDF and CDF are related by the fact that the CDF is the integral of the PDF.
The PDF and CDF are both important tools used in probability and statistics to describe and analyze data.
