Velocity, a core concept in physics, offers a window into the dynamics of motion, be it of an object hurtling through space or the earth itself spinning on its axis. It’s a measure that captures both the speed and direction of an object’s movement. While often discussed in a general sense, velocity manifests in two distinct forms: linear and angular. Each serves as a pillar in understanding how objects move in different scenarios, from the simplest mechanisms to complex natural phenomena.
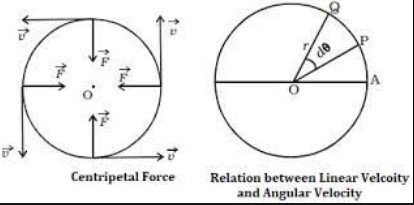
The relationship between linear velocity and angular velocity is straightforward: linear velocity measures how fast an object moves along a path, and angular velocity quantifies how quickly it rotates around a central point or axis. The two are intrinsically linked by the radius of the rotation, where linear velocity equals the angular velocity multiplied by the radius of the circular path.
Diving deeper, this connection underpins many aspects of our daily lives and the broader universe. It’s present in the design of vehicles, the functioning of various mechanical devices, the performance of athletes, and even the celestial dance of planets and stars. Understanding this relationship not only enriches one’s knowledge of physics but also unveils the underlying principles governing both man-made and natural movements.
Basic Concepts
Velocity Defined
Velocity, in its broadest sense, represents the speed of an object along with its direction of movement. It’s a vector quantity, meaning it has both magnitude and direction. Velocity helps us quantify how fast something is moving and in which direction it is headed. This concept is foundational in the realms of physics and engineering, providing a basis for understanding various aspects of motion and dynamics.
Definition of Velocity
At its core, velocity measures the rate of change of an object’s position with respect to time. It’s calculated by dividing the distance traveled by the time it takes to travel that distance, incorporating the direction to the equation.
Types: Linear and Angular
Velocity manifests in two primary forms: Linear and Angular. Linear velocity pertains to objects moving in a straight line or along a curve, while Angular velocity relates to objects rotating around an axis.
Linear Velocity
Concept and Formula
Linear velocity describes the rate at which an object moves through space. It’s calculated using the formula:
�=��v=td
where �v is the linear velocity, �d is the distance covered, and �t is the time taken to cover that distance.
Units of Measurement
The standard unit for measuring linear velocity is meters per second (m/s), though other units like kilometers per hour (km/h) may also be used depending on the context.
Examples in Real Life
- A car moving at 60 km/h along a highway
- A person walking at 1.5 m/s in a park
Angular Velocity
Concept and Formula
Angular velocity quantifies how quickly an object rotates or spins around a fixed axis. Its formula is given by:
�=��ω=tθ
where �ω is the angular velocity, �θ is the angle of rotation (in radians), and �t is the time taken for the rotation.
Units of Measurement
Angular velocity is typically measured in radians per second (rad/s). However, degrees per second can also be used.
Examples in Real Life
- The Earth rotating about its axis, completing a rotation (360° or 2�2π radians) every 24 hours
- A record player’s disc spinning at **33\frac{1}{3}) revolutions per minute (RPM)
The Link
Connection Explained
The relationship between linear and angular velocity is crucial in understanding how objects move in circular paths or rotations. This connection is elegantly captured by the formula:
�=��v=rω
where �v is the linear velocity, �r is the radius of the circular path, and �ω is the angular velocity. This equation shows that linear velocity is proportional to the angular velocity and the radius of the path.
How Linear and Angular Velocity Relate
The formula �=��v=rω highlights that for any point on a rotating object, its linear velocity is determined by how quickly the object is spinning (angular velocity) and how far the point is from the axis of rotation (radius). This means that points farther from the axis move faster (higher linear velocity) even if the object spins at a constant rate (angular velocity).
The Formula Connecting Both
This pivotal formula, �=��v=rω, bridges the concepts of linear and angular velocity, enabling the translation of rotational motion into linear terms and vice versa. It’s a key principle in designing and analyzing systems involving rotational movement, such as gears, wheels, and turbines.
Factors Influencing Relationship
Radius of Rotation
The radius of rotation significantly impacts the linear velocity for a given angular velocity. A larger radius means that an object will have a higher linear velocity at the same rate of rotation.
Speed of the Object
The speed at which an object rotates (angular velocity) directly influences its linear velocity. An increase in angular velocity results in a proportional increase in linear velocity, assuming the radius of rotation remains constant.

Practical Applications
In Machinery
Gears and Pulleys
Gears and pulleys are fundamental components in various machinery, transforming power and motion efficiently. The relationship between linear and angular velocity is key to designing these systems for optimal performance. For example, in a bicycle, the gear system converts the angular velocity of pedaling into the linear velocity of the bike’s movement, enabling it to travel faster or climb hills with less effort.
- Efficiency Calculations: By adjusting the radius (size) of gears and pulleys, engineers can precisely control the output speed and force, optimizing the machinery for specific tasks, such as lifting heavy loads or achieving high speeds.
Calculations for Efficiency
Efficiency in machinery often hinges on the correct application of linear and angular velocities. For instance, the efficiency of a conveyor belt system can be enhanced by adjusting the diameter of the drive pulleys to alter the belt’s speed without changing the motor’s speed, thereby conserving energy and reducing operational costs.
In Sports
Ball Games and Athletes
In sports like baseball, cricket, or golf, understanding the connection between linear and angular velocities can significantly impact performance. For a baseball pitcher, the spin rate (angular velocity) of the ball can affect its trajectory and speed (linear velocity), influencing how difficult it is for the batter to hit.
- Enhancing Performance: Coaches and athletes use insights from physics to improve techniques, such as optimizing the angle and speed of a soccer kick or the spin of a tennis ball, to achieve desired outcomes in the game.
In Nature
Planetary Movements
The motion of planets around the sun is a grand illustration of linear and angular velocities at play. Earth’s orbit involves a constant angular velocity but, due to its elliptical path, its linear velocity varies, being fastest when closest to the sun (perihelion) and slowest when farthest (aphelion).
- Impact on Seasons and Tides: The Earth’s rotation (angular velocity) and its translation around the sun (linear velocity) are critical in determining seasonal changes and tidal patterns, affecting climate, weather, and the natural world.
Calculations and Examples
Step-by-Step Guide
How to Calculate Linear Velocity from Angular
To calculate the linear velocity from angular velocity, you can use the formula:
�=��v=rω
- Step 1: Identify the angular velocity (�ω) of the object in radians per second.
- Step 2: Determine the radius (�r) of the rotation or path.
- Step 3: Multiply the angular velocity by the radius to find the linear velocity.
How to Calculate Angular Velocity from Linear
The process can be reversed to find angular velocity from linear velocity:
�=��ω=rv
- Step 1: Identify the linear velocity (�v) of the object.
- Step 2: Determine the radius (�r) of the rotation or path.
- Step 3: Divide the linear velocity by the radius to find the angular velocity.
Real-world Problems
Examples Involving Calculations
- Example 1: A car tire has a diameter of 0.6 meters. If the tire rotates at 10 radians per second, what is the car’s linear velocity? Using �=��v=rω, the linear velocity is 0.3×10=30.3×10=3 m/s.
- Example 2: A satellite orbits Earth at a linear velocity of 7,800 m/s at a distance of 20,000 km from the center. The angular velocity can be calculated by �=��ω=rv, resulting in an angular velocity of approximately 0.000390.00039 rad/s.
Applying the Formula in Different Scenarios
The formula �=��v=rω is versatile, applicable in designing roller coasters to ensure safety at high speeds, in robotics to control the precise movement of arms and joints, and even in the animation industry to create realistic movements.
Key Takeaways
Summary of Important Points
- Velocity is a vector quantity that describes the rate and direction of an object’s movement.
- There are two types: Linear velocity for motion along a path, and Angular velocity for rotation around an axis.
- The formula �=��v=rω connects the two, highlighting the dependence of linear velocity on the radius of rotation and the rate of spinning.
- This relationship has practical applications in machinery, sports, and the natural world, influencing design, performance, and our understanding of planetary movements.
The Significance of Understanding This Relationship
Understanding the relationship between linear and angular velocity enriches our comprehension of the physical world and enables advancements across various fields. From the precise engineering of mechanical systems to enhancing athletic performance and grasping the cosmic dance of celestial bodies,
Frequently Asked Questions
How Do Linear and Angular Velocity Differ?
Linear velocity pertains to the rate at which an object moves from one point to another in a straight or curved path, measured in units like meters per second. Angular velocity, on the other hand, describes the rate of rotation around a central axis, typically measured in radians per second. The key difference lies in their focus: linear velocity on straightforward movement, and angular velocity on rotational motion.
Can You Convert Angular Velocity to Linear Velocity?
Yes, angular velocity can be converted to linear velocity through the formula: linear velocity = angular velocity x radius of the rotation. This conversion is crucial in various fields, such as engineering and sports science, to understand and predict the motion of rotating objects and their impact on linear movement.
Why Is Understanding the Relationship Between Linear and Angular Velocity Important?
Grasping the relationship between linear and angular velocity is vital for several reasons. It enables the design and analysis of mechanical systems, improves strategies in sports, aids in the study of planetary motion, and enhances our comprehension of the physical laws governing motion. This understanding is foundational for advancements in technology, sports, and our grasp of the universe’s workings.
Conclusion
The exploration of linear and angular velocity sheds light on the intricate dance of motion that pervades our universe, from the spin of a top to the orbit of planets. This relationship is not just a cornerstone of physics but a testament to the interconnectedness of motion in all its forms. By understanding how linear and angular velocities relate, we unlock a deeper appreciation for the principles that govern our physical world and the myriad ways they manifest in both the natural and engineered environments.
Furthermore, this knowledge equips us with the tools to innovate, optimize, and problem-solve across a broad spectrum of applications. Whether it’s enhancing the performance of a machine, improving athletic techniques, or broadening our understanding of cosmic movements, the insights gained from the relationship between linear and angular velocity continue to propel us forward in our quest for comprehension and mastery of the world around us.

