The concepts of differentiability and continuity lie at the heart of calculus, serving as fundamental tools for analyzing and understanding the behavior of functions. These concepts help mathematicians and scientists describe the way functions behave at specific points, and how they can be graphed across intervals. The relationship between these two mathematical properties is crucial for a wide range of applications, from engineering to economics.
Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. Simply put, a function must be continuous at a point for it to be differentiable there. However, the converse is not always true; a function can be continuous at a point without being differentiable there. This fundamental relationship underscores the nuanced behavior of functions in calculus.
The distinction and relationship between these two properties are more than just theoretical interest; they provide essential insights into the function’s graph and behavior. Understanding how and why these concepts are related allows for deeper analysis of functions, helping to predict and explain their real-world behavior. This insight is invaluable for both academic research and practical applications in various fields.

Defining Continuity
Basic Concept of Continuity
Continuity is a fundamental concept in calculus that describes how a function behaves at a certain point and across intervals. When we say a function is continuous, we mean that there are no breaks, jumps, or sharp points in its graph at that point or over a given interval. In simpler terms, you can draw the function without lifting your pen from the paper.
Conditions for Continuity
For a function �(�)f(x) to be considered continuous at a point �=�x=a, it must satisfy three conditions:
- Function is Defined: �(�)f(a) must exist.
- Limit Exists: The limit of �(�)f(x) as �x approaches �a must exist, denoted as lim�→��(�)limx→af(x).
- Limit Equals Function Value: The limit of the function as �x approaches �a must equal the function value at �a, i.e., lim�→��(�)=�(�)limx→af(x)=f(a).
These conditions ensure that at point �a, the function smoothly passes without any interruption.
Visual Understanding
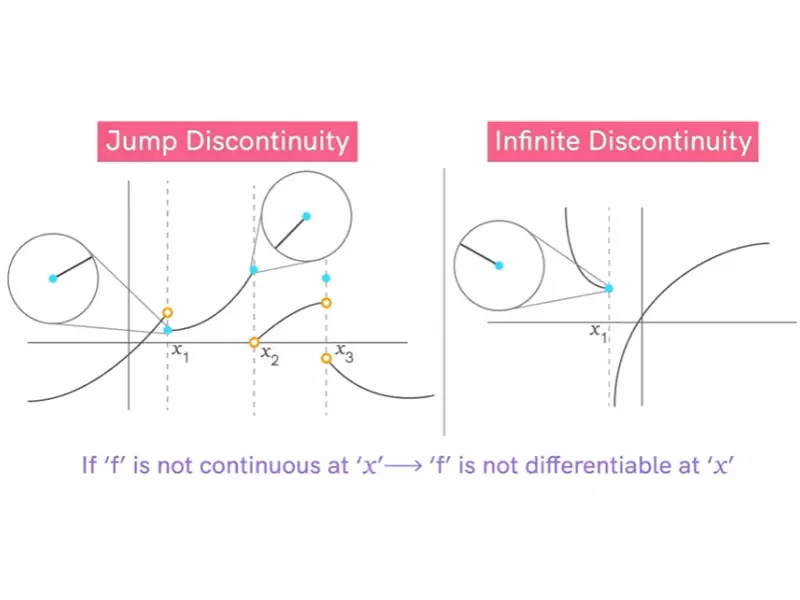
Imagine graphing a function that smoothly curves without any gaps or jumps. This visual representation helps understand continuity intuitively. Graphs with holes, jumps, or vertical asymptotes at a point indicate discontinuity at that point.
Defining Differentiability
Basic Concept of Differentiability
Differentiability goes a step beyond continuity by not only looking at how a function behaves but how it changes at a point or over an interval. A function is differentiable at a point if it has a defined derivative there, meaning the function’s rate of change at that point is clear and precise. Differentiability provides a way to measure how a function’s output value changes as its input value changes, represented by the slope of the tangent line to the function at that point.
Conditions for Differentiability
A function �(�)f(x) is differentiable at a point �=�x=a if:
- It is continuous at �=�x=a. A function cannot be differentiable at a point where it is not continuous.
- The derivative of �(�)f(x) at �=�x=a exists. This means the limit limℎ→0�(�+ℎ)−�(�)ℎlimh→0hf(a+h)−f(a) exists and is finite.
These conditions confirm that the function has a well-defined tangent at �=�x=a, indicating a smooth change in the slope.
Visual Understanding
Visualizing differentiability involves looking for places where a function has a clear, defined slope or direction. If you can “zoom in” on any part of the function and eventually see a straight line, the function is differentiable at that point. Conversely, points with corners, cusps, or vertical tangents indicate where a function is not differentiable.
Core Relation
Continuity as a Prerequisite
Continuity is a necessary condition for differentiability. A function must first be continuous at a point for it to be differentiable there. This means all differentiable functions are continuous, but not all continuous functions are differentiable.
Differentiability Implies Continuity
Since a function must be continuous to be differentiable, we can say that differentiability implies continuity. This is a fundamental concept in understanding the behavior of functions in calculus.
Exceptions to the Rule
While differentiability always implies continuity, there are functions that are continuous at every point but not differentiable at certain points. These exceptions often occur at points where the function has a sharp turn or cusp.
Deep Dive: Why Differentiability Implies Continuity
Mathematical Proof
The proof of why differentiability implies continuity is rooted in the definition of the derivative. Given that the derivative of �(�)f(x) at �=�x=a exists, the limit of the difference quotient as ℎh approaches zero exists and is finite. This inherently means that the function must approach a specific value as �x approaches �a, fulfilling the criteria for continuity.
Intuitive Explanation
Intuitively, if a function changes smoothly and predictably at a point (as indicated by its differentiability), then there can’t be any sudden jumps or gaps at that point. The very nature of having a defined rate of change (derivative) implies that the function behaves nicely enough to not have abrupt interruptions in its path.
Exploring Exceptions
Continuous but Not Differentiable
A function can be smooth and uninterrupted (continuous) while still having points where its rate of change is undefined or not consistent (not differentiable). These points are often characterized by sharp angles or cusps in the graph.
Classic Examples
- The Absolute Value Function (∣�∣∣x∣) is continuous everywhere but not differentiable at �=0x=0 because it has a sharp corner at the origin.
- The Weierstrass Function is a more complex example of a function that is continuous everywhere but differentiable nowhere, illustrating how wildly a function can behave while still being continuous.
Practical Implications
Understanding the relationship between differentiability and continuity is not just an academic exercise. It has profound implications in various fields, influencing how professionals approach problems and develop solutions.
Real-world Applications
Differentiability and continuity play a crucial role in engineering, economics, and physics. For example, in mechanical engineering, the design of a component must account for how force and displacement relate to each other, often requiring continuous and differentiable functions to predict behavior under stress accurately. In economics, differentiable functions are used to model behaviors like cost, revenue, and profit maximization, providing clarity on how small changes in input can affect output.
Significance in Mathematical Modeling
Mathematical modeling heavily relies on these concepts to simulate real-world phenomena accurately. The ability to use continuous and differentiable functions allows for the creation of models that can predict weather patterns, stock market trends, and the spread of diseases. The precision of these models depends on understanding the nuances of continuity and differentiability, ensuring they mimic real-life behaviors as closely as possible.
Continuity without Differentiability
While many functions are both continuous and differentiable, some are continuous at every point but not differentiable at certain points. These exceptions highlight the complexity of function behavior.
Graphical Insights
Graphically, a continuous but not differentiable function might have a sharp corner or a cusp. Consider the graph of the absolute value function, which is smooth and continuous but has a sharp turn at the origin, making it non-differentiable at that point. These visual cues are vital for identifying potential issues in mathematical models or physical systems.
Understanding Non-Differentiable Points
Non-differentiable points are critical in applications where the rate of change is essential for predictions or optimizations. In materials science, for example, understanding where a stress-strain curve becomes non-differentiable can indicate potential failure points in materials under stress.
Differentiability in Higher Dimensions
The concept of differentiability extends beyond single-variable functions to functions of multiple variables, crucial for fields like quantum mechanics, fluid dynamics, and multivariable calculus.
Extension to Multivariable Functions
In multivariable calculus, a function is differentiable if it is differentiable in each of its variables and if the partial derivatives are continuous across the function’s domain. This extension allows for the analysis of surfaces and solids in three dimensions, providing a deeper understanding of their properties.
Differences in Conditions and Implications
The conditions for differentiability become more complex in higher dimensions. For a function of two variables to be differentiable, not only must it be continuous, but its partial derivatives must also exist and be continuous around the point of interest. This ensures that the function behaves smoothly and predictably in all directions from that point.
Theoretical Insights
The theories behind continuity and differentiability are rooted in the concept of limits, a fundamental building block of calculus.
The Role of Limits
Limits describe how a function behaves as it approaches a particular point, underpinning both continuity and differentiability. A function is continuous if the limit of the function as it approaches a point is equal to the function’s value at that point. Similarly, a function is differentiable at a point if the limit defining the derivative at that point exists. This foundational role of limits highlights their importance in understanding and applying calculus concepts.
Advanced Concepts in Differentiability
As we delve deeper into calculus, we encounter more advanced concepts like smoothness and analyticity. A function is considered smooth if it is differentiable to all orders, meaning it has derivatives of all degrees that are continuous. Analytic functions, a subset of smooth functions, can be represented by a power series in a neighborhood of any point in their domain. These advanced concepts provide further insights into the behavior of functions and their applications in complex problems.
Frequently Asked Questions
What is Continuity in Calculus?
Continuity in calculus refers to a function’s smooth progression without breaks, jumps, or sharp turns at a point or over an interval. For a function to be considered continuous at a point, it must meet three criteria: the function is defined at the point, the limit of the function as it approaches the point exists, and the function’s value at that point equals the limit.
How is Differentiability Related to Continuity?
Differentiability is a concept that builds upon continuity, focusing on a function’s ability to have a derivative at a point. For a function to be differentiable at a point, it must first be continuous there. This requirement stems from the nature of derivatives, which represent the function’s rate of change at a point. If a function is not continuous, it cannot have a well-defined rate of change, hence it cannot be differentiable at that point.
Can a Function be Continuous Everywhere but Not Differentiable?
Yes, a function can be continuous everywhere but not differentiable at certain points. A classic example of such a function is the absolute value function, which is continuous across its entire domain. However, it is not differentiable at the origin (x=0) because it has a sharp corner there, disrupting the smooth change in slope that is required for differentiability.
Why are Non-Differentiable Points Important?
Non-differentiable points are important because they represent places where the behavior of a function changes fundamentally, such as corners or cusps on a graph. These points can indicate transitions in the function’s behavior, marking areas of potential interest for further investigation, especially in applied mathematics and physics where such changes can have significant real-world implications.
Conclusion
The exploration of differentiability and continuity reveals the intricate dance between these two foundational concepts in calculus. They serve as essential tools for understanding the behavior of functions, offering insights into how functions grow, change, and react under various conditions. The requirement that a function be continuous to be differentiable, yet not necessarily the reverse, highlights the nuanced nature of mathematical analysis.
Recognizing the relationship and differences between differentiability and continuity is more than an academic exercise; it’s a critical aspect of applying calculus to solve real-world problems. This understanding enables the development of more accurate models, predictions, and analyses in fields as diverse as physics, engineering, economics, and beyond, illustrating the profound impact of mathematical principles on our understanding of the world.
