Calculus stands as a monumental pillar in the vast landscape of mathematics, weaving together the intricate concepts of change, motion, and growth. At its core, the study of calculus branches into two essential ideas: continuity and differentiability. These concepts serve not just as foundational stones for theoretical mathematics but also as critical tools for a multitude of applications across physics, engineering, economics, and beyond.
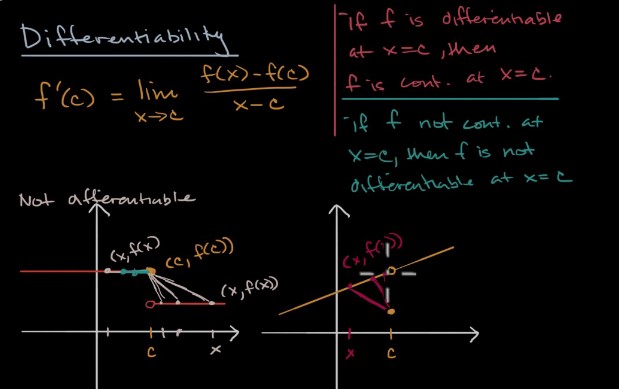
The relation between continuity and differentiability can be succinctly described as follows: while a differentiable function must always be continuous, a continuous function is not necessarily differentiable. This principle hinges on the understanding that differentiability, which concerns the existence of a function’s derivative, implies a smoother behavior than continuity, which merely requires a function to be unbroken.
Continuity and differentiability together form the backbone of calculus, offering a framework to analyze and understand the behavior of functions. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by ensuring that functions have a defined slope at each point. This distinction is crucial for the precise prediction and modeling of natural phenomena, where smooth transitions and predictable changes are often essential for accuracy.
Basics of Continuity
Definition and Intuition
Continuity in mathematics refers to the smooth flow of a function without any breaks, jumps, or sudden changes in direction. For a function to be continuous at a particular point, you should be able to draw its graph at that point without lifting your pencil off the paper.
For example, consider the function �(�)=�2f(x)=x2. This function is continuous because, for every value of �x you choose, �(�)f(x) gives a corresponding output without any gaps or jumps. You can plot its graph smoothly from start to finish.
Conditions for Continuity
For a function �(�)f(x) to be considered continuous at a point �c in its domain, three conditions must be met:
- The point �c must be in the domain of �f.
- The limit of �(�)f(x) as �x approaches �c must exist.
- The limit of �(�)f(x) as �x approaches �c must be equal to �(�)f(c).
In simple terms, these conditions ensure that the function is defined at �c, approaches a specific value as �x gets closer to �c, and that this specific value is the actual value of the function at �c.
Basics of Differentiability
Definition and Understanding
A function is differentiable at a point if it has a defined derivative at that point. The derivative represents the rate of change of the function’s output with respect to its input. In essence, if you can calculate how steeply a function’s graph is sloping at any given point, that function is differentiable at that point.
Take the function �(�)=�2f(x)=x2 again. It is differentiable everywhere because, at every point on its graph, you can determine how steep the graph is. For any value of �x, the derivative of �(�)f(x), denoted as �′(�)f′(x), gives us the slope of the tangent line to the graph at that point.
Conditions for Differentiability
A function �(�)f(x) is differentiable at a point �c if:
- The function is continuous at �c. A function must not have any breaks or sharp turns at the point �c.
- The derivative �′(�)f′(c) exists. This means you can calculate a unique slope of the tangent to the graph of �f at �c.
If a function meets these criteria, it smoothly transitions at �c, and you can define its rate of change at that exact point.
Exploring the Connection
Continuity as a Prerequisite
Continuity is a prerequisite for differentiability. This is because, for a function to have a rate of change at a point, that point must first be part of a smooth curve without any breaks. If a function is not continuous at a point, we cannot even begin to discuss its slope there, as the concept of slope becomes meaningless.
Differentiability Implies Continuity
While a differentiable function must be continuous, a continuous function may not always be differentiable. The implication of differentiability includes continuity because the existence of a derivative at a point necessitates a well-defined, uninterrupted path through that point. However, a function can be smooth and unbroken (continuous) without having a clear direction (derivative) at every point.
Visualizing the Relationship
Graphical Representations
Graphs provide a powerful way to visualize the relationship between continuity and differentiability. A continuous function without any breaks forms a single, unbroken curve when plotted. When a function is also differentiable, this curve does not have any sharp corners; it smoothly transitions from one point to the next, allowing for the calculation of a slope or tangent line at any point.
Examples and Counterexamples
Examples of Continuous but Not Differentiable Functions:
- Absolute Value Function: �(�)=∣�∣f(x)=∣x∣ is continuous everywhere but not differentiable at �=0x=0 because it has a sharp point at this location.
- Weierstrass Function: This function is famous for being continuous everywhere but nowhere differentiable. Its graph looks like a tangled, unending sea wave, showcasing that continuity does not guarantee differentiability.
These examples highlight that while continuity ensures a function is unbroken, differentiability demands more – a smooth transition that permits the definition of a slope at every point.
Applications in Real World
In Engineering and Physics
Continuity and differentiability are cornerstone concepts in engineering and physics, integral to modeling and solving complex problems. For instance, in mechanical engineering, the design of a machine component requires smooth, continuous curves without abrupt changes, ensuring stress distribution is even and predictable. Similarly, in fluid dynamics, a field within physics, the behavior of fluids is modeled using differential equations that necessitate the fluid’s velocity field to be differentiable, thereby predicting flow patterns and identifying potential turbulence sites accurately.
In the realm of electrical engineering, signal processing relies on differentiable functions to design filters and circuits that respond predictably to varying inputs. The continuity of electrical signals is paramount for the seamless transmission and reception in communication systems, avoiding data loss or corruption.
In Economics and Other Fields
Economics and finance heavily utilize these mathematical principles to model economic growth, optimize investment strategies, and forecast market trends. Continuity ensures that small changes in economic indicators lead to predictable outcomes, facilitating long-term planning and stability in financial markets. Differentiability, on the other hand, allows economists to calculate marginal costs and benefits, crucial for determining optimal production levels and pricing strategies.
Beyond these, fields such as computer science, especially in algorithms involving gradient descent for optimization, and in geology, where modeling the earth’s continuous but varied surface properties, also rely on these concepts.
Advanced Topics
Functions with Discontinuities
While most real-world phenomena can be modeled using continuous functions, there are instances where discontinuities cannot be ignored. Functions that are continuous except at certain points are particularly interesting in both theoretical and applied mathematics. For example, a manufacturing process might have a cost function that is continuous within specific intervals but experiences jumps due to sudden changes in material costs or machinery efficiency at certain production levels. Understanding these discontinuities is essential for accurately modeling the cost and optimizing production.
The Role of Limits
The concept of limits is fundamental to understanding both continuity and differentiability. A limit describes the behavior of a function as it approaches a specific point from both directions. In the context of continuity, a function is continuous at a point if the limit of the function as it approaches that point is equal to the function’s value at that point. For differentiability, the existence of a limit of the difference quotient as the interval approaches zero is key. This deep dive reveals how limits not only underpin the formal definitions of these concepts but also facilitate their practical application across various scenarios.
Common Misunderstandings
Misinterpretation of Concepts
A frequent misunderstanding is conflating continuity with differentiability. While related, these concepts are distinct. A continuous function does not necessarily have a derivative at every point within its domain, as illustrated by functions that are smooth and uninterrupted but have sharp corners or vertical tangents at certain points. Clarifying this distinction is crucial for correctly applying these concepts in mathematical modeling and problem-solving.
Avoiding Pitfalls in Application
To avoid common mistakes when applying concepts of continuity and differentiability, consider these guidelines:
- Always verify the conditions for continuity and differentiability before proceeding with calculations.
- Be mindful of points where functions transition from one formula to another, as these are common locations for discontinuities or non-differentiability.
- Utilize graphical analysis as a preliminary tool for identifying potential issues with continuity and differentiability before delving into analytical methods.
FAQs
What is Continuity in Mathematics?
In mathematics, continuity refers to the property of a function that allows it to have no breaks, jumps, or gaps in its domain. For a function to be continuous at a particular point, it must meet three criteria: the point must be in the function’s domain, the function must have a limit at that point, and the function’s value at that point must equal its limit.
How Does Differentiability Relate to Continuity?
Differentiability and continuity are closely linked; for a function to be differentiable at a point, it must first be continuous at that point. However, continuity alone does not guarantee differentiability. Differentiability requires that a function not only be continuous but also have a well-defined tangent at every point within its domain, signifying a smooth transition without any sharp corners or vertical tangents.
Can a Function be Continuous Everywhere but not Differentiable?
Yes, a function can be continuous at every point in its domain but not be differentiable everywhere. A classic example is the absolute value function, which is continuous everywhere but not differentiable at the point where its graph makes a sharp turn. This illustrates that while continuity ensures no gaps in the function, it does not necessarily imply smoothness or the presence of a derivative.
Why is the Study of Continuity and Differentiability Important?
The study of continuity and differentiability is vital for understanding and predicting the behavior of functions, which is essential in modeling real-world phenomena. These concepts allow mathematicians and scientists to ensure that functions behave predictably without sudden changes, which is crucial for applications in physics, engineering, economics, and other fields where precise calculations are necessary.
Conclusion
The dance between continuity and differentiability in mathematics is a delicate balance that reveals the nuanced behavior of functions. While continuity ensures that functions flow without interruption, differentiability adds a layer of smoothness, providing a deeper understanding of how functions change at each point. This intricate relationship underscores the complexity and beauty of calculus, demonstrating its pivotal role in not only theoretical mathematics but also in practical applications across a spectrum of disciplines.
Through exploring the relation between continuity and differentiability, we gain valuable insights into the fundamental principles that govern the natural and scientific worlds. It is this understanding that enables us to model and predict with accuracy, pushing the boundaries of what we can achieve in science, engineering, and beyond. The journey through calculus, marked by the study of these concepts, is not just an academic pursuit but a venture into the essence of how the universe operates.

