Epidemiological models such as SIR and SEIR play crucial roles in understanding the spread of infectious diseases and in planning public health responses. These models help scientists and policymakers predict how diseases like influenza or COVID-19 will spread through populations and what measures might effectively control an outbreak. They are fundamental tools in epidemiology, used to simulate the dynamics of infection among a population over time.
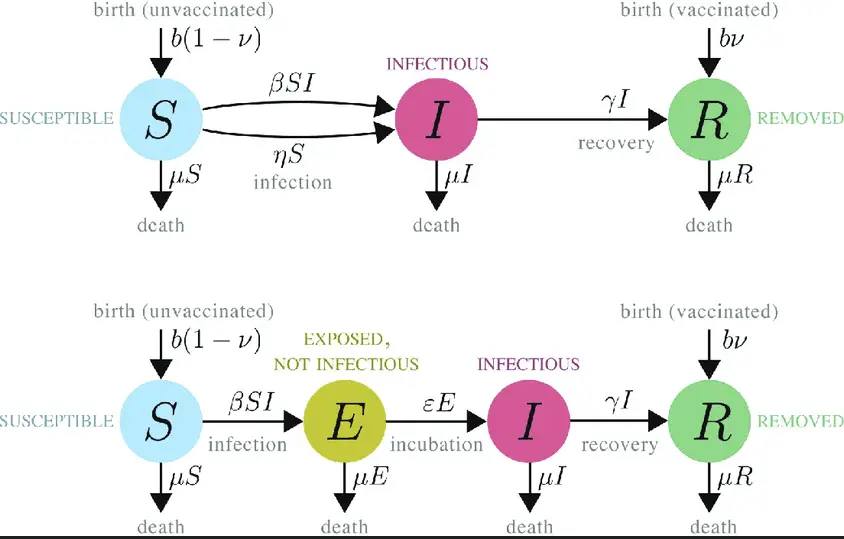
The SIR model segments a population into three categories: Susceptible, Infectious, and Recovered. It provides a framework to track the number of people in each category, assuming that recovered individuals gain immunity. The SEIR model adds an additional category, Exposed, which accounts for individuals who have been infected but are not yet infectious. This distinction allows the SEIR model to more accurately represent diseases with an incubation period.
Epidemic models, by quantifying the parameters of disease transmission and recovery, offer insights into the likely course of an outbreak. They help identify potential hotspots of infection and evaluate the impact of public health interventions like vaccination and social distancing. This is especially critical in managing diseases that require time to show symptoms, making the SEIR model particularly valuable in such scenarios.
Epidemic Modeling Basics
What Are Epidemic Models?
Epidemic models are mathematical representations that simulate the spread of infectious diseases within a population over time. These models are crucial for predicting how a disease spreads and assessing the potential effectiveness of public health interventions to control or mitigate an epidemic. They form the backbone of epidemiological research, aiding in the understanding of disease dynamics and guiding public health decisions.
Key Components of Models
At their core, epidemic models consist of several key components:
- Population Groups: Models divide the population into distinct groups based on disease status—such as susceptible, infected, and recovered.
- Transition Rates: These are rates at which individuals move between groups, influenced by factors like contact rates and recovery times.
- Initial Conditions: The state of the population at the start of the simulation, including the number of infected and susceptible individuals.
- Parameters: These include transmission coefficients and recovery rates, which define how quickly a disease spreads and recovers within the population.
The SIR Model
Definition and Components
The SIR model is a classic framework used in epidemiology to describe the spread of diseases without immunity. SIR stands for Susceptible, Infectious, and Recovered. It assumes that individuals in a population can only be in one of these three states and that transitions between these states occur with certain probabilities which are determined by the parameters of the model.
How the SIR Model Works
The SIR model operates by tracking the number of individuals in each state over time:
- Susceptible (S): Individuals who can contract the disease.
- Infectious (I): Individuals who have the disease and can transmit it to the susceptible.
- Recovered (R): Individuals who have recovered from the disease and are immune to it.
The model uses differential equations to describe how individuals move from being susceptible to infectious and then to recovered, based on the transmission rate and recovery rate.
Use Cases of SIR Model
The SIR model has been used extensively to model various infectious diseases, especially those where recovery confers lasting immunity. It is commonly applied to:
- Influenza outbreaks
- Measles transmission
- Smallpox scenarios
The SEIR Model
Definition and Components
The SEIR model adds another layer to the classic SIR model by including an Exposed (E) category. This category represents individuals who have been infected but are not yet infectious, which is crucial for diseases that have a significant incubation period.
How the SEIR Model Works
The SEIR model enhances the SIR model by introducing the following stages:
- Exposed (E): Individuals who have been infected but are not yet infectious.
- The transitions now include a rate at which exposed individuals become infectious, reflecting the incubation period of the disease.
This additional stage allows for more accurate modeling of diseases like COVID-19, where there is a delay between infection and the ability to infect others.
Differences from SIR Model
The main difference between the SIR and SEIR models lies in the inclusion of the exposed state in the SEIR model. This difference allows the SEIR model to account for the latency period of the infection, providing a more nuanced understanding of the disease’s dynamics.
Comparing SIR and SEIR
Similarities Between the Models
Both models are compartmental and use differential equations to model the transitions between different disease states. They share a common purpose: to predict and analyze the spread of infectious diseases through populations.
Key Differences
The key difference is the inclusion of an Exposed state in the SEIR model, which adds complexity but increases accuracy for diseases with an incubation period.
Practical Applications
Both models are used by health organizations and researchers to predict disease outbreaks and assess intervention strategies. The choice between SIR and SEIR often depends on the specific characteristics of the disease being modeled, such as the presence of an incubation period.
Model Dynamics
Transition Rates and Variables
In epidemic modeling, transition rates are crucial for understanding how quickly a disease can spread through a population. These rates, represented by parameters in the model’s equations, determine the speed at which individuals move from one state (such as susceptible) to another (like infected). Key variables include:
- Transmission Rate: The likelihood of transmission per contact between a susceptible and an infected individual.
- Recovery Rate: The rate at which infected individuals recover and gain immunity or die.
- Contact Rate: The number of contacts per person per time unit that could result in a disease transmission.
These variables are fundamental in shaping the predictions of epidemic models and in strategizing public health responses.
Impact of Latent Infection (SEIR)
The latent infection phase in the SEIR model acknowledges a period where individuals are infected but not yet infectious. This stage is critical for diseases with a noticeable incubation period, such as COVID-19, where individuals can carry and transmit the virus without showing symptoms immediately. This aspect of the model allows for more accurate forecasting and intervention planning, helping to curb the spread at an asymptomatic level.
Recovery and Immunity
Recovery and immunity are pivotal in controlling the outbreak of any infectious disease. The SIR and SEIR models assume that after recovering from the infection, individuals gain immunity and do not get infected again. This assumption is vital for predicting the end of an epidemic and understanding potential for herd immunity:
- Permanent Immunity: Often assumed in models like SIR where recovered individuals do not return to the susceptible state.
- Temporary Immunity: Some models consider a waning immunity, where recovered individuals can become susceptible again.
Mathematical Formulation
Basic Equations of SIR
The SIR model is governed by a set of differential equations that describe the rate of change in each compartment. The basic equations are:
- 𝑑𝑆𝑑𝑡=−𝛽𝑆𝐼𝑁dtdS=−βNSI
- 𝑑𝐼𝑑𝑡=𝛽𝑆𝐼𝑁−𝛾𝐼dtdI=βNSI−γI
- 𝑑𝑅𝑑𝑡=𝛾𝐼dtdR=γI
Here, 𝛽β represents the transmission rate, 𝛾γ the recovery rate, and 𝑁N the total population.
Basic Equations of SEIR
The SEIR model extends the SIR equations by adding an exposed compartment. The equations for the SEIR model are:
- 𝑑𝑆𝑑𝑡=−𝛽𝑆𝐼𝑁dtdS=−βNSI
- 𝑑𝐸𝑑𝑡=𝛽𝑆𝐼𝑁−𝜎𝐸dtdE=βNSI−σE
- 𝑑𝐼𝑑𝑡=𝜎𝐸−𝛾𝐼dtdI=σE−γI
- 𝑑𝑅𝑑𝑡=𝛾𝐼dtdR=γI
In these equations, 𝜎σ represents the rate at which exposed individuals become infectious.
Comparative Analysis
Comparing these models shows how adding an exposed state can delay the peak of an epidemic, providing critical time for interventions. The SEIR model typically shows a slower spread initially due to the incubation period, leading to different strategic responses in public health planning.
Applications in Real-World Scenarios
Historical Epidemics
Models like SIR and SEIR have been applied to historic epidemics to understand their spread and control. For instance, the SIR model helped analyze the 1918 influenza pandemic, while SEIR models have been used to study the dynamics of more recent outbreaks like SARS and H1N1 influenza.
Modern-Day Applications
Today, these models are integral to managing diseases such as COVID-19. They help in simulating various scenarios and answering what-if questions regarding intervention strategies, such as social distancing, vaccinations, and lockdown measures.
Predictive Accuracy and Limitations
While highly useful, these models have limitations. Their accuracy depends on the quality and availability of data, assumptions about disease dynamics, and changes in population behavior over time. Predictive accuracy can be compromised by these factors, necessitating continuous refinement of the models as new data becomes available.
Model Selection Criteria
When to Use SIR vs. SEIR
Choosing between the SIR and SEIR models depends on the disease’s characteristics. For diseases with a significant incubation period, the SEIR model is preferable as it can model the delay between infection and infectiousness.
Factors Influencing Model Choice
- Nature of the Disease: Incubation period, mode of transmission, and presence of immunity.
- Available Data: Quality and completeness of data regarding disease spread and population behavior.
- Intended Use: Whether the model is used for predictive purposes or for understanding disease dynamics.
Examples of Decision Making
In decision-making scenarios, such as during the COVID-19 pandemic, public health officials used SEIR models to plan and implement lockdowns and social distancing measures based on predictions of disease spread and health system capacity.
Frequently Asked Questions
What is an epidemic model?
Epidemic models are mathematical frameworks that describe the spread of infectious diseases in populations. These models estimate how diseases transmit from one person to another and assess the impact of public health interventions.
How does the SIR model function?
The SIR model categorizes a population into Susceptible, Infectious, and Recovered individuals. It uses differential equations to describe the rates at which individuals move between these categories, providing insights into disease dynamics and the effects of interventions.
What adds the ‘E’ in SEIR model?
In the SEIR model, the ‘E’ stands for Exposed. It represents individuals who have been infected but are not yet infectious. This category allows the model to account for the incubation period of diseases, offering a more detailed analysis of disease spread.
Why use the SEIR model over SIR?
The SEIR model is used over the SIR model when dealing with diseases that have a significant incubation period during which the infected individuals are not infectious but will become so. This allows for more accurate predictions and planning in public health scenarios.
How do these models aid public health?
These models help public health officials predict and manage the spread of diseases, plan interventions, and allocate resources efficiently. By understanding the potential progression of an outbreak, better preventative measures can be implemented.
Conclusion
Epidemic models like SIR and SEIR are indispensable in the toolbox of epidemiologists and public health authorities. They provide a scientific basis for predicting disease spread and evaluating the potential effectiveness of control strategies. Through these models, it is possible to anticipate the course of an epidemic and implement measures that can significantly alter its impact.
The ongoing development and refinement of these models are vital for preparedness and response in public health. As new diseases emerge and old ones evolve, understanding and applying these models in real-world scenarios will continue to be a critical element of global health security.