The exploration of atomic spectra has been a cornerstone in the understanding of atomic and quantum physics. Specifically, the study of spectral lines, which are essentially the fingerprints of elements in the universe, has revealed much about the structure of atoms and molecules. Among the tools developed to decipher these spectral lines, the Rydberg and Balmer formulas stand out for their historical and scientific significance, particularly in relation to the hydrogen spectrum.
The difference between the Rydberg and Balmer formulas lies in their application and scope. The Balmer formula is a specific case of the Rydberg formula, applied to calculate the visible spectral lines of the hydrogen atom. The Rydberg formula, on the other hand, is a more general equation that can predict the wavelengths of not only the hydrogen spectrum but also the spectra of other elements under certain conditions.
The Balmer formula was the first to provide a mathematical understanding of the hydrogen spectrum, specifically its visible light emissions. It was later encapsulated by the more general Rydberg formula, which expanded the understanding to a wider range of electromagnetic radiation. These formulas are not merely equations but tools that have deepened our understanding of the quantum world, bridging gaps in knowledge from the micro to the macro scales of the universe.
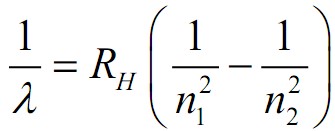
Spectral Lines Basics
Atomic Spectra
The atomic spectra are a physical phenomenon that appears as discrete lines on a high-resolution spectrogram. Each element emits or absorbs light at very specific wavelengths, leading to the creation of these unique spectral lines. The atomic spectra play a crucial role in physics, chemistry, and astronomy, serving as a fingerprint for identifying elements in various states of matter, whether in a distant star or a laboratory on Earth.
Key Points:
- Atomic spectra are unique to each element.
- They result from electrons moving between energy levels within an atom.
- Their study is essential for understanding atomic structure.
Hydrogen Spectrum
The hydrogen spectrum is a particularly important part of atomic spectra, mainly because hydrogen is the simplest and most abundant element in the universe. This spectrum includes several series of lines, named after their discoverers, and is visible under specific conditions when hydrogen gas is excited.
Specific Focus:
- The hydrogen spectrum consists of lines in the ultraviolet (Lyman series), visible (Balmer series), and infrared (Paschen series, Brackett series, and others) regions.
- These spectral lines are produced when electrons in the hydrogen atom transition between energy levels.
The Balmer Series
Discovery
The Balmer series was discovered by Johann Jakob Balmer in 1885. Balmer, a Swiss mathematician, found a formula that accurately calculated the visible spectral lines of the hydrogen atom. His discovery was groundbreaking, as it provided the first step towards understanding the quantized nature of electron transitions in atoms.
History Points:
- Balmer’s work was initially empirical.
- His formula was the first to predict the wavelengths of the hydrogen spectrum accurately.
Formula Explanation
Balmer’s formula can be written as �=�(�2�2−22)λ=B(n2−22n2), where �λ is the wavelength of the emitted light, �B is the Balmer constant, and �n is the principal quantum number (an integer greater than 2). This formula was crucial because it laid the groundwork for the later development of the Rydberg formula.
Formula Components:
- �λ: Wavelength of emitted light
- �B: Balmer constant
- �n: Principal quantum number
Application
The Balmer series has several important applications in both physics and astronomy. In physics, it is used to understand the electronic structure of atoms, while in astronomy, it helps in identifying hydrogen in stars and galaxies.
Applications Include:
- Determining the composition of stars.
- Studying the interstellar medium.
Rydberg Formula
Genesis
The Rydberg formula was proposed by the Swedish physicist Johannes Rydberg in 1888, building upon Balmer’s work. Rydberg generalized Balmer’s formula to calculate the wavelengths of all the spectral lines of hydrogen, not just those in the visible spectrum. His work marked a significant advancement in atomic physics, introducing a universal method to predict the spectral lines of hydrogen.
Development Points:
- Rydberg aimed to create a universal formula for spectral lines.
- His formula was instrumental in the development of quantum mechanics.
Mathematical Form
The Rydberg formula is given by 1�=��(1�12−1�22)λ1=RH(n121−n221), where �λ is the wavelength of the emitted light, ��RH is the Rydberg constant for hydrogen, and �1n1 and �2n2 are integers where �2>�1n2>n1. This formula can predict the wavelengths of the spectral lines emitted by hydrogen atoms when an electron transitions from a higher energy level (�2n2) to a lower energy level (�1n1).
Formula Components:
- �λ: Wavelength of emitted light
- ��RH: Rydberg constant for hydrogen
- �1,�2n1,n2: Principal quantum numbers
Universality
The Rydberg formula‘s universality extends beyond the hydrogen spectrum, as it can also predict the spectral lines of other elements under certain conditions. This universality makes the Rydberg formula a powerful tool in spectroscopy, aiding in the study of various elements and their ions.
Universal Aspects:
- Applicable to single-electron ions like He+, Li2+, etc.
- Fundamental in understanding atomic structures across the periodic table.
Key Differences
Scope of Application
The Rydberg formula and the Balmer formula are both pivotal in the study of spectral lines, yet they differ significantly in their scope of application. The Balmer formula specifically calculates the wavelengths of the visible spectral lines of the hydrogen atom, making it a specialized tool for studying a narrow yet important range of electromagnetic radiation. On the other hand, the Rydberg formula serves a broader purpose, offering a method to calculate the wavelengths of not only the hydrogen spectrum but also the spectral lines of other elements, provided they can be approximated to a hydrogen-like model.
Key Points:
- Balmer formula: Limited to visible spectral lines of hydrogen.
- Rydberg formula: Applies to a wider range of elements and spectra.
Mathematical Complexity
While both formulas stem from similar theoretical backgrounds, their mathematical complexity differs. The Balmer formula is relatively simple and straightforward, making it easily accessible to students and researchers starting in spectroscopy. Conversely, the Rydberg formula introduces a level of complexity that requires a deeper understanding of quantum mechanics and atomic physics. The inclusion of more variables and its broader applicability mean that the Rydberg formula can appear more daunting but also more versatile.
Comparison:
- Balmer formula: Simpler, easier for beginners.
- Rydberg formula: More complex, versatile for advanced studies.
Predictive Accuracy
The predictive accuracy of these formulas is another area where differences emerge. The Balmer formula, within its scope, provides extremely accurate predictions for the visible spectral lines of hydrogen. However, the Rydberg formula, due to its generalized nature, can sometimes yield less precise results for complex atoms or ions. The precision of the Rydberg formula is unparalleled when applied to hydrogen and hydrogen-like systems, showcasing the power of a more generalized approach.
Insights:
- Balmer formula: Highly accurate within its limited scope.
- Rydberg formula: Broadly accurate, with some limitations in complex systems.
Practical Implications
In Astronomy
The study of astronomy has been revolutionized by the ability to analyze the spectral lines of distant stars and galaxies. The Balmer series, in particular, is a critical tool in identifying hydrogen in astronomical objects, given its strong presence in visible light. The Rydberg formula extends this capability, allowing astronomers to identify various elements and ions across the electromagnetic spectrum. This ability is crucial for understanding the composition, temperature, density, and movement of astronomical bodies.
Role in Observations:
- Balmer series: Essential for studying star compositions.
- Rydberg formula: Facilitates broader spectral analysis.
In Quantum Mechanics
The development of quantum mechanics owes much to the insights provided by the study of spectral lines. The quantization of energy levels, a foundational principle of quantum mechanics, was first suggested by the patterns observed in the hydrogen spectrum and later generalized through the application of the Rydberg formula. These formulas not only supported the theoretical framework of quantum mechanics but also provided empirical evidence crucial for its acceptance.
Contributions:
- Balmer series and Rydberg formula: Empirical bases for quantization.
- Facilitated the development of quantum mechanics.
Recent Advances
Modifications and Refinements
Over time, both the Balmer and Rydberg formulas have undergone significant modifications and refinements. Advances in quantum physics and computational methods have led to more accurate versions of these formulas. These improvements account for factors like electron spin, relativistic corrections, and quantum defects in multi-electron atoms, enhancing the predictive power and applicability of these spectral formulas.
Recent Developments:
- Enhanced accuracy with quantum and relativistic corrections.
- Broader applicability to complex atomic systems.
Technological Applications
The implications of these formulas extend far beyond academic inquiry, finding applications in various technologies. Spectroscopy, powered by the principles derived from the Balmer and Rydberg formulas, is fundamental in industries ranging from pharmaceuticals to semiconductor manufacturing. Techniques such as laser spectroscopy and astronomical spectroscopy rely on these formulas to identify chemical compositions, assess physical conditions, and even detect distant exoplanets.
Modern Applications:
- Laser spectroscopy: Uses precise wavelength predictions for material analysis.
- Astronomical spectroscopy: Identifies chemical compositions of celestial bodies.
Frequently Asked Questions
What is the Balmer Series?
The Balmer series consists of the spectral emission lines of the hydrogen atom that fall within the visible light spectrum. Discovered by Johann Balmer in 1885, this series arises when an electron in a hydrogen atom falls from a higher energy level to the second energy level, producing visible light.
How does the Rydberg Formula differ from the Balmer Formula?
The Rydberg formula is a general equation used to predict the wavelengths of the spectral lines of many chemical elements, including hydrogen. In contrast, the Balmer formula is a specific case of the Rydberg formula that calculates the wavelengths of the visible spectral lines of hydrogen.
Why are these formulas important in physics?
These formulas are crucial for understanding the structure of atoms and the behavior of electrons in different energy states. They provide a quantitative description of the spectral lines emitted by atoms, which is fundamental to the fields of quantum mechanics, atomic physics, and astronomy.
Can the Rydberg Formula be used for elements other than hydrogen?
Yes, the Rydberg formula can be applied to other elements, especially for calculating the spectral lines of single-electron ions such as He+, Li2+, and so forth. However, its application becomes more complex with multi-electron atoms due to electron-electron interactions.
Conclusion
The Rydberg and Balmer formulas are not just mathematical curiosities; they are fundamental to our understanding of the atomic world. They have provided a quantitative framework that supports the conceptual foundations of quantum mechanics and atomic physics. Through these formulas, we have been able to decode the mysteries of the hydrogen atom, paving the way for discoveries in various fields of science.
Moreover, the historical journey from the Balmer formula to the Rydberg formula exemplifies the evolution of scientific thought, from specific observations to general laws. These equations have not only enriched our scientific knowledge but also underscored the interconnectedness of the universe, from the smallest atom to the vast expanses of the cosmos.

