Histograms serve as foundational tools in the realm of statistics and data analysis, offering a graphical representation of data distribution across different intervals. These visual aids are instrumental in simplifying complex data sets, allowing for a more straightforward interpretation of the underlying patterns and trends. By categorizing data into bins or intervals, histograms provide a clear picture of frequency distribution, making it easier to identify the concentration of data points and the spread of data values.
The primary distinction between a relative frequency histogram and a frequency histogram lies in the way data is represented. While a frequency histogram plots the count of data points within each bin, a relative frequency histogram displays the proportion or percentage of the data that falls into each category. This fundamental difference affects not only the construction of these histograms but also their interpretation and application in various statistical analyses.
Frequency histograms are particularly useful in highlighting the absolute numbers of observations within each bin, offering a direct insight into the dataset’s composition. In contrast, relative frequency histograms excel in comparing distributions from different sized samples by normalizing the data, thereby facilitating a comparative analysis across diverse datasets. This distinction underscores the importance of selecting the appropriate histogram type based on the analytical context and objectives.
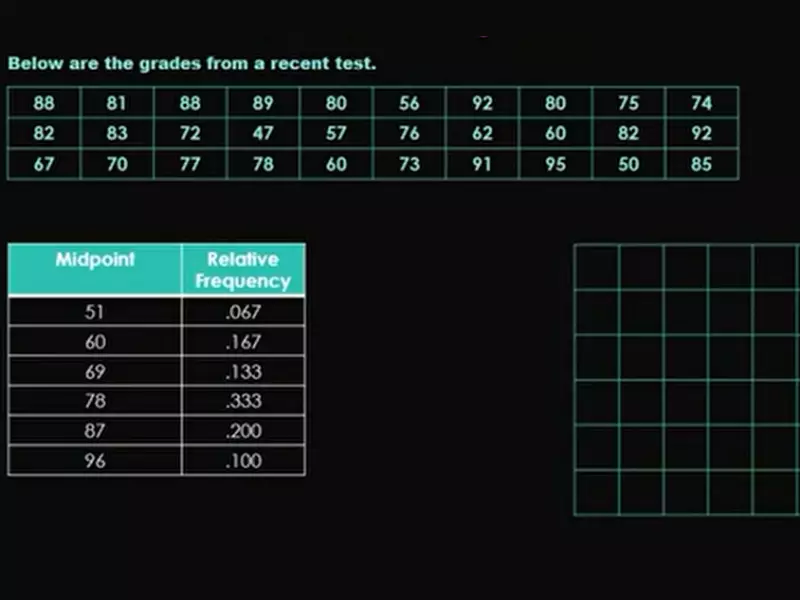
Histogram Basics
Definition and Purpose
A histogram is a graphical representation that organizes a group of data points into user-specified ranges. Each bar in a histogram represents the tabulated frequency at each interval/bin, which makes it an invaluable tool in statistics and data analysis for visually summarizing the distribution, variability, and central tendency of data.
Histograms are significant because they provide a quick way to understand the distribution of a dataset. By displaying the frequency of data points within certain ranges, histograms can reveal patterns such as skewness towards high or low values, the presence of multiple modes in the data, and the spread of the data across its range.
Components of a Histogram
Bars and Intervals
- Bars: Each bar in a histogram represents the frequency of data within a specific interval. The height of the bar corresponds to the frequency count of data points falling within that interval.
- Intervals: Also known as bins, intervals divide the entire range of data into a series of non-overlapping segments. The choice of interval size can significantly affect the histogram’s appearance and interpretability.
Axis Labels and Titles
- Axis Labels: Essential for understanding a histogram, the horizontal (x-axis) typically represents the data categories or intervals, while the vertical (y-axis) shows the frequency count.
- Titles: A clear, descriptive title helps to quickly convey the purpose of the histogram to the viewer, enhancing its communicative value.
Frequency Histograms
Overview
A frequency histogram is a type of histogram that uses vertical bars to show the frequency of data points that fall within each of several ranges of values. It is a powerful tool for data representation and helps in identifying the distribution and frequency of data points within a dataset.
Use Cases and Examples
Frequency histograms are widely used across various fields such as economics, healthcare, and education to analyze and visualize data distributions. For example, a teacher may use a frequency histogram to represent the distribution of test scores in a class, helping to quickly identify how many students achieved certain score ranges.
Construction
Steps to Create a Frequency Histogram
- Collect Data: Gather the dataset you want to analyze.
- Determine Intervals: Decide the number and size of intervals or bins.
- Tally Frequencies: Count the number of data points in each interval.
- Draw Bars: For each interval, draw a bar that represents its frequency.
Choosing Intervals and Counting Occurrences
- Intervals: The choice should balance detail and clarity, with too few intervals oversimplifying the data and too many making it cluttered.
- Occurrences: Counting how many data points fall into each interval is crucial for determining the height of each bar.
Interpretation
Understanding a frequency histogram involves recognizing patterns such as uniformity, skewness, or the presence of outliers. These patterns can indicate underlying characteristics of the dataset, like central tendency and variability.
Common Patterns and Their Meanings
- Symmetrical Distribution: Indicates that data is evenly distributed around a central value.
- Skewed Distribution: Suggests an asymmetry in the data distribution, with a tail that extends to either the right (positive skew) or left (negative skew).
Relative Frequency Histograms
Overview
Unlike frequency histograms, relative frequency histograms display the proportion or percentage of data points that fall within each interval relative to the total dataset. This approach is particularly useful when comparing datasets of different sizes.
Definition and Differentiation from Frequency Histograms
A relative frequency histogram provides a view of the data distribution in terms of relative or proportional frequencies, offering a normalized perspective that is especially beneficial when comparing distributions across different sample sizes.
When to Use a Relative Frequency Histogram
This type of histogram is ideal when the focus is on the proportion of observations within each interval rather than the absolute number of observations. It’s particularly useful in comparative studies and normalizing data from different datasets.
Construction
Creating a Relative Frequency Histogram
- Calculate Relative Frequencies: Divide the frequency of each interval by the total number of data points to get the relative frequency.
- Plot Bars: Plot bars where the height corresponds to the relative frequency of each interval.
Calculating Relative Frequencies
The relative frequency of each interval is calculated by dividing the number of data points in the interval by the total number of data points in the dataset. This is usually expressed as a percentage.
Interpretation
Analyzing a relative frequency histogram involves understanding the proportion of data within each interval as part of the whole. This can provide insights into the relative importance of different intervals within the dataset.
Benefits Over Frequency Histograms in Certain Scenarios
Relative frequency histograms are particularly useful in scenarios where datasets of different sizes are being compared, or where the focus is on the proportion of the dataset that falls within certain ranges rather than the absolute frequencies.

Key Differences
Data Representation
Absolute vs. Relative Data Comparison
The core distinction between frequency histograms and relative frequency histograms lies in their approach to data representation. Frequency histograms present absolute values, counting the number of occurrences within each interval. In contrast, relative frequency histograms display relative values, showing the proportion or percentage of the total data that falls within each interval. This fundamental difference significantly impacts the interpretation of the data, with frequency histograms providing a straightforward count and relative frequency histograms offering a comparative perspective across different or varying-sized datasets.
Impact on Interpretation
The choice between absolute and relative data presentation affects how we interpret the data. Frequency histograms are excellent for identifying the sheer volume of data points within intervals, which is particularly useful in datasets of a uniform size. Relative frequency histograms, however, excel in contexts where understanding the distribution’s proportionality is crucial, such as when comparing datasets of different sizes or when the focus is on the distribution pattern rather than the count.
Use Cases
Scenarios where one is preferred over the other
Choosing between a frequency histogram and a relative frequency histogram depends on the specific needs of the data analysis. Frequency histograms are preferred when the goal is to understand the frequency of occurrences within a dataset of a single dimension or size. They are ideal for analyzing the distribution of a singular dataset where comparative analysis isn’t required.
Relative frequency histograms are favored in comparative analysis scenarios, where datasets of different sizes are involved, or when the focus is on the proportion of occurrences within each bin relative to the whole dataset. This makes them especially useful in studies where normalization of data is necessary to facilitate comparisons.
Examples from various fields
In education, a frequency histogram could be used to visualize the number of students scoring within certain grade intervals on a specific test. Conversely, a relative frequency histogram would be better suited to compare grade distributions across different classes of varying sizes. In healthcare, frequency histograms might show the number of patients visiting a clinic per day, while relative frequency histograms could compare the proportion of different diagnoses among patients across various clinics.
Advantages and Limitations
Strengths and Weaknesses of Each Type
Frequency histograms are straightforward and provide a clear picture of how many data points fall into each interval, making them excellent for single dataset analysis. However, their utility diminishes when comparing across datasets of different sizes, as they do not account for relative proportions.
Relative frequency histograms, on the other hand, highlight the proportion of data within each interval, offering a normalized view that facilitates comparison across datasets. This normalization, while beneficial for comparative analysis, may obscure the actual volume of data points within each interval, which could be a limitation when absolute numbers are critical to the analysis.
Selecting the right histogram based on data analysis needs
The decision to use a frequency or relative frequency histogram should be guided by the objectives of the data analysis. When absolute numbers and their distributions within a dataset are of primary interest, frequency histograms are the go-to. For comparative analysis or when dealing with datasets of varying sizes, relative frequency histograms offer a more insightful perspective.
Selecting the Right Histogram
Factors to Consider
Data type and volume
The nature and volume of the data at hand are critical considerations. Large datasets and those requiring comparative analysis across different groups or conditions are better served by relative frequency histograms. In contrast, smaller, single datasets where the focus is on the distribution of data points themselves benefit more from frequency histograms.
Analysis goals
The ultimate goal of the analysis should dictate the type of histogram used. For instance, if the objective is to compare the distribution of a particular variable across different populations, a relative frequency histogram is more appropriate. However, if the aim is to understand the frequency distribution within a single population, a frequency histogram will suffice.
Guidelines for Selection
Practical tips for choosing between the two types
- Evaluate the data size and type: Consider whether your data lends itself more to absolute or relative comparison.
- Define your analysis goals: Clearly outline what you hope to achieve with your data analysis to guide your choice of histogram.
- Consider your audience: Think about who will be viewing the histogram and what information they need to extract from it.
Avoiding common mistakes
- Overlooking data volume: Failing to account for the size of your datasets can lead to misleading interpretations if the wrong type of histogram is chosen.
- Ignoring analysis goals: Not aligning the histogram type with the analysis objectives can result in an ineffective representation of the data.
- Misinterpreting the histograms: Ensure that the chosen histogram type is interpreted correctly, keeping in mind the differences between absolute and relative frequencies.
Frequently Asked Questions
What is a frequency histogram?
A frequency histogram is a graphical representation that displays the number of observations within each of a series of intervals, or bins. It helps in visualizing the distribution of data points across these bins, making it easier to identify patterns such as the central tendency, dispersion, and skewness of the data.
How does a relative frequency histogram differ from a frequency histogram?
A relative frequency histogram differs from a frequency histogram by the way it represents data. Instead of showing the absolute number of observations in each bin, it displays the proportion or percentage of the total observations that fall within each bin. This approach allows for easier comparison of datasets of different sizes or scales.
When should I use a relative frequency histogram?
A relative frequency histogram should be used when the goal is to compare the distribution of data sets of different sizes or when it is important to understand the proportion of the total represented by each bin. It is particularly useful in comparing the relative outcomes of different groups, highlighting underlying patterns without the distraction of varying group sizes.
Can I convert a frequency histogram to a relative frequency histogram?
Yes, you can convert a frequency histogram to a relative frequency histogram by calculating the proportion or percentage of each bin’s count relative to the total number of observations. This conversion allows analysts to view data distributions in terms of relative frequencies, facilitating comparisons across different datasets.
Conclusion
Understanding the distinction between relative frequency histograms and frequency histograms is crucial for anyone engaged in statistical analysis or data interpretation. These two types of histograms serve different purposes and provide unique insights into the data. While frequency histograms are invaluable for assessing the absolute numbers within each bin, relative frequency histograms offer a comparative perspective, highlighting the proportion of data within each category relative to the whole.
Choosing the appropriate histogram is essential for accurate and meaningful data analysis. This decision should be guided by the specific objectives of the analysis, whether it’s to understand the raw distribution of data or to compare distributions across varying sample sizes. By applying the right type of histogram, analysts can unlock deeper insights into their data, enabling informed decisions and compelling presentations of statistical findings.
