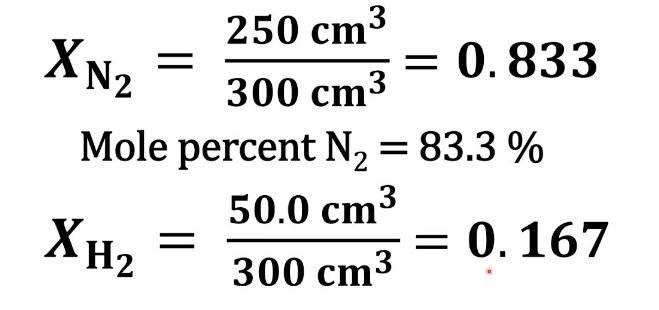When exploring the realm of chemistry and materials science, understanding the composition of mixtures is fundamental. Among the various measures of concentration, mole fraction and weight percent stand out due to their wide applications across different fields. These concepts not only aid in the precise formulation of chemical solutions but also play a critical role in industrial processes, pharmaceuticals, and analytical chemistry.
Mole fraction is a dimensionless quantity representing the ratio of the number of moles of a component to the total number of moles of all components in the mixture. On the other hand, weight percent (or weight/weight percent) is a measure that indicates the mass of a solute as a percentage of the total mass of the solution. Both methods serve as essential tools for chemists and engineers to describe the concentration of components in mixtures accurately.
Diving into their specifics, mole fraction and weight percent are utilized based on the nature of the mixture and the required precision in measurements. While mole fraction is often preferred in theoretical and gas-related calculations due to its temperature independence, weight percent is commonly used in solutions where the physical weight plays a significant role, such as in the food, pharmaceutical, and materials industries. Understanding the difference between these two measures is crucial for professionals to make informed decisions in research, development, and quality control processes.

Basic Concepts
Mole Fraction
Definition and formula
The mole fraction is a dimensionless quantity representing the ratio of the number of moles of a component to the total number of moles of all components in the mixture. The formula for calculating the mole fraction, denoted by �χ, is as follows:
��=��������χi=ntotalni
where ��χi is the mole fraction of component �i, ��ni is the number of moles of component �i, and ������ntotal is the total number of moles of all components in the mixture.
How to calculate
To calculate the mole fraction:
- Identify the number of moles of each component in the mixture.
- Sum up the moles of all components to find ������ntotal.
- Divide the moles of the component of interest by ������ntotal.
- Repeat for each component if needed.
Weight Percent
Definition and formula
Weight percent (wt%), also known as mass percent, is a measure that indicates the mass of a solute as a percentage of the total mass of the solution. The formula for calculating weight percent is:
��%�=(��������������)×100wt%i=(masstotalmassi)×100
where ��%�wt%i is the weight percent of component �i, �����massi is the mass of component �i, and ���������masstotal is the total mass of the mixture.
Calculation method
To determine the weight percent:
- Weigh the mass of each component.
- Add these masses to get ���������masstotal.
- Divide the mass of the component of interest by ���������masstotal and multiply by 100.
- Perform this calculation for each component if necessary.
Key Differences
Conceptual Framework
Basis of measurement
The main difference between mole fraction and weight percent lies in their basis of measurement. Mole fraction is based on the number of moles, a measure of quantity without considering mass. In contrast, weight percent is based on mass, providing a direct indication of the weight of each component relative to the total.
Unit considerations
Mole fraction is a unitless measure, making it universally applicable without the need for conversion between units of mass. Weight percent, however, is expressed as a percentage, directly relating the mass of components to the total mass.
Calculation Contrast
Steps in calculation
Calculating mole fraction and weight percent involves different steps:
- For mole fraction:
- Determine the number of moles of each component.
- Calculate the total number of moles in the mixture.
- Divide the moles of each component by the total number of moles.
- For weight percent:
- Measure the mass of each component.
- Sum up to find the total mass of the mixture.
- Calculate the ratio of each component’s mass to the total mass and multiply by 100.
Examples for clarity
- Mole fraction example: A mixture contains 2 moles of A and 3 moles of B. The mole fraction of A (��χA) is 22+3=0.42+32=0.4.
- Weight percent example: In a solution with 40g of solute and 160g of solvent, the weight percent of the solute is (4040+160)×100=20%(40+16040)×100=20%.
Application Scope
Preferred contexts for each
- Mole fraction is often preferred in gas mixtures and when dealing with reactions to easily relate to stoichiometry without the influence of temperature or pressure.
- Weight percent is widely used in solutions where the physical properties of the mixture, like density or viscosity, are important, making it ideal for formulations in industries.
Industry standards
- In pharmaceuticals, weight percent is crucial for ensuring the correct dosage and consistency of products.
- Chemical engineering often relies on mole fraction for process calculations, especially in the design and analysis of separation processes like distillation.

Practical Implications
Analytical Chemistry
Role in substance analysis
In analytical chemistry, accurately determining the composition of a mixture is crucial. The use of mole fraction and weight percent varies based on the nature of the analysis.
- Mole fraction is essential in gas chromatography and spectroscopy, where the focus is on the mole ratio of components. It helps in identifying and quantifying substances in a mixture by providing a clear measure of their relative quantities without the influence of their masses.
- Weight percent, on the other hand, is widely used in titrations and when preparing standard solutions. Its direct relation to the mass makes it indispensable for analyses that rely on precise mass measurements, such as in gravimetric analysis.
Pharmaceutical Applications
Dosage formulations
The formulation of dosages in the pharmaceutical industry hinges on accurate concentration measurements. Both mole fraction and weight percent play vital roles.
- Mole fraction can be critical in the development of gas anesthetics, where the precise control over the ratio of gases ensures efficacy and safety.
- Weight percent is more commonly used in the formulation of solid and liquid dosages, such as tablets, creams, and liquid medicines. It ensures that each dosage unit contains the correct amount of active ingredients, critical for patient safety and treatment effectiveness.
Manufacturing Processes
Mixture preparation
In manufacturing, preparing mixtures with exact specifications is often required.
- In the chemical industry, mole fraction is used in the synthesis of compounds where reactants must be mixed in precise stoichiometric ratios.
- Weight percent is prevalent in industries such as food processing and materials manufacturing, where the consistency of the product depends on the mass ratio of ingredients. It is crucial for achieving the desired texture, strength, or flavor in products.
Advantages and Limitations
Mole Fraction
Pros and cons
Pros:
- Independence from temperature and pressure makes mole fraction ideal for gas mixtures and theoretical studies.
- Simplicity in stoichiometric calculations in chemical reactions, as it directly relates to the number of particles.
Cons:
- Not intuitive for everyday applications where mass is a more familiar concept.
- Less useful in heterogeneous mixtures where the phases have significantly different densities.
Weight Percent
Benefits and drawbacks
Benefits:
- Intuitive and practical, especially in formulations where the mass of ingredients is directly relevant.
- Versatility in application across a wide range of industries, including food, pharmaceuticals, and materials.
Drawbacks:
- Temperature and pressure sensitivity can affect measurements, particularly in gas mixtures.
- Not suitable for stoichiometric calculations in reactions without additional conversion steps.
Choosing the Right Measure
Factors to consider
When deciding between mole fraction and weight percent, several factors need to be considered:
- Nature of the mixture: Gas mixtures favor mole fraction, while solutions and solids often use weight percent.
- Purpose of the calculation: For theoretical and stoichiometric purposes, mole fraction may be more appropriate. For practical and formulation tasks, weight percent is usually preferred.
- Industry standards: Adhering to the common practices in your field can ensure consistency and comparability of results.
Tips for accurate application
To ensure the accurate application of mole fraction and weight percent, consider the following tips:
- Understand the basics: Grasping the fundamental differences and applications of each measure can guide the initial choice.
- Check calculations: Whether calculating mole fraction or weight percent, double-checking calculations can prevent errors that might impact the results significantly.
- Consider the context: The specific requirements of your project or experiment, such as precision, ease of measurement, and industry norms, should guide your choice.
- Practice with examples: Applying both measures in practice problems can build familiarity and help recognize when each is most appropriately used.
Frequently Asked Questions
What is a mole fraction?
A mole fraction is a unitless measure that expresses the proportion of a constituent to the total amount of all constituents in a mixture. It is calculated by dividing the number of moles of the constituent by the total number of moles present in the mixture. This method is particularly useful for gas mixtures and when temperature and pressure conditions are a consideration.
How do you calculate weight percent?
Weight percent is determined by taking the mass of a component and dividing it by the total mass of the mixture, then multiplying by 100 to convert it into a percentage. This concentration measurement is widely used in formulations where the mass of ingredients is critical, such as in manufacturing, cooking, and pharmaceutical preparations.
Why is mole fraction used instead of weight percent in gases?
Mole fraction is often used over weight percent for gases because it is independent of temperature and pressure changes. This makes it an ideal choice for calculations and predictions in situations where gases are involved, ensuring consistency and accuracy in results regardless of external conditions.
Can mole fraction and weight percent give the same value?
In certain conditions, mole fraction and weight percent can give similar values, especially in dilute solutions or when the molar masses of the solute and solvent are close. However, due to the fundamental differences in their calculation bases—number of moles versus mass—such occurrences are more the exception than the rule.
Conclusion
The journey through the concepts of mole fraction and weight percent unravels the intricacies involved in measuring and understanding the composition of mixtures. These two measures, each with its unique advantages and applications, offer chemists and industry professionals the tools needed to accurately define the concentration of components, ensuring precision in scientific research and industrial processes.
In conclusion, whether it’s the dimensionless purity of mole fraction ideal for gas mixtures and theoretical calculations, or the practical mass-based clarity of weight percent vital for solutions and manufacturing, recognizing the appropriate context for their application is crucial. This knowledge empowers professionals to achieve desired outcomes with efficiency and precision, highlighting the importance of these fundamental concepts in the vast field of chemistry and beyond.