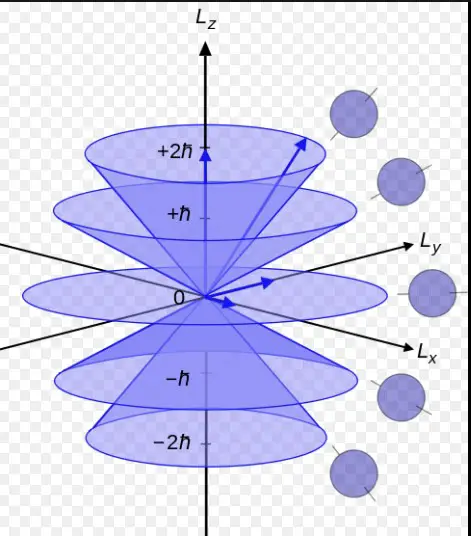
Quantum numbers are fundamental to the understanding of quantum mechanics, serving as the “DNA” of electrons within atoms. They provide a comprehensive framework for predicting electron behavior, defining their energy levels, and how they occupy orbitals. Each quantum number offers unique information about the electron’s position and movement, critical for chemists and physicists alike to decode the intricate dance of particles at the subatomic level.
The principal quantum number and azimuthal quantum number are two such key identifiers, each playing distinct roles. The principal quantum number, symbolized as �n, primarily determines the energy level and size of the electron’s orbit. In contrast, the azimuthal quantum number, denoted as �l, dictates the shape of the orbital and, indirectly, the electron’s angular momentum. Together, they lay the groundwork for understanding the electron’s precise location and its energy characteristics within an atom.
Diving deeper, the principal quantum number (�n) and the azimuthal quantum number (�l) not only influence the energy and shape of electron orbitals but also affect observable physical and chemical properties of atoms and molecules. These properties include the atom’s size, its energy emissions in spectroscopy, and its behavior in chemical bonding. Grasping the nuances of these quantum numbers is essential for unraveling the complexities of atomic and molecular structures, predicting chemical reactions, and designing materials and drugs with specific properties.
Quantum Numbers Explained
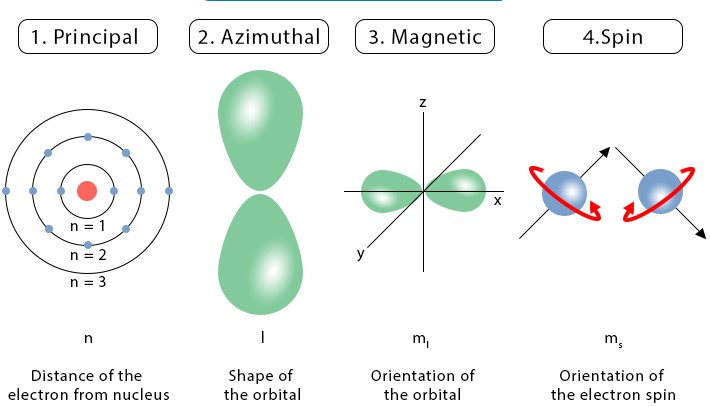
Quantum numbers are like the addresses of electrons within an atom. These numbers not only tell us where an electron is but also give insights into its behavior. There are four quantum numbers, but here we’ll focus on two: the principal quantum number (n) and the azimuthal quantum number (l). Understanding these will help you grasp how electrons occupy the space around an atom’s nucleus and their energy levels.
Principal Quantum Number
Definition and Symbol
The principal quantum number, symbolized as �n, is the first quantum number. It identifies the energy level of an electron in an atom. Think of it as the floor number in a high-rise building, where higher floors correspond to higher energy levels.
Role in Defining Electron’s Energy Level
The principal quantum number directly influences an electron’s energy. Electrons in higher energy levels (�n) are further from the nucleus and have higher energy. This concept is foundational in quantum mechanics and chemistry, affecting how atoms absorb and emit energy.
Impact on Atom’s Size and Energy
An atom’s size increases with the principal quantum number. Higher �n values mean electrons are further away from the nucleus, making the atom larger. The energy of the atom also increases as �n increases, because electrons gain energy as they move to higher levels.
Variability and Allowed Values
The principal quantum number can take any positive integer value (�=1,2,3,…n=1,2,3,…). The lowest value (�=1n=1) corresponds to the closest energy level to the nucleus, which has the lowest energy.
Azimuthal Quantum Number
Definition and Symbol
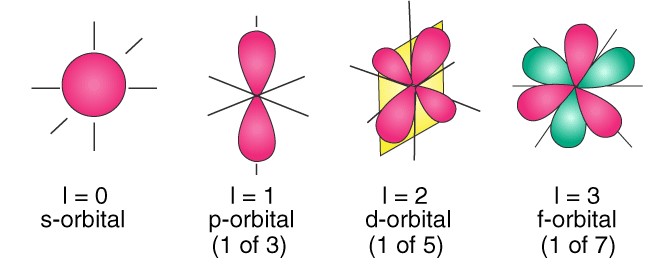
The azimuthal quantum number, denoted as �l, indicates the shape of the orbital where an electron resides. Orbitals can be thought of as the different apartment layouts on each floor of our high-rise building analogy.
Connection to Electron’s Angular Momentum
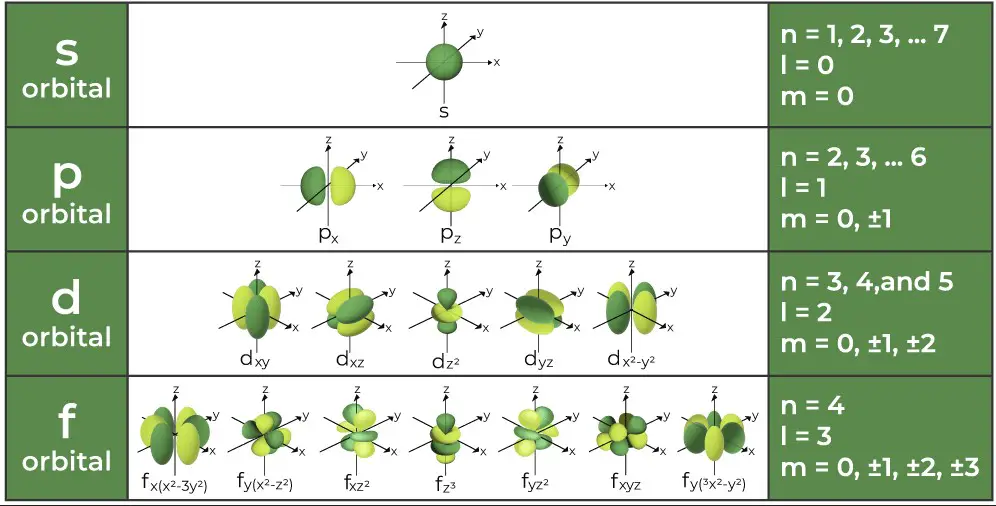
The azimuthal quantum number is associated with the angular momentum of an electron. This momentum is a measure of its circular motion around the nucleus. Different �l values correspond to different types of orbitals (s, p, d, f), each with a unique shape.
Determination of Orbital Shape
The value of �l determines the shape of the electron’s orbital, affecting the distribution of electrons in space. These shapes are crucial for understanding the chemical bonding and reactivity of atoms.
Allowed Values and Significance
The azimuthal quantum number �l ranges from 0 to �−1n−1 for each value of �n. For example, if �=3n=3, �l can be 0, 1, or 2, corresponding to s, p, and d orbitals, respectively. Each value of �l introduces a new orbital type, significantly increasing the complexity and capacity of an atom’s electron cloud.
Core Differences
Energy Levels and Orbitals
The principal quantum number (�n) and azimuthal quantum number (�l) together shape our understanding of where electrons can be found around the nucleus and their energy levels. While �n sets the stage by determining the energy level, �l refines the plot by specifying the orbital shape within that level.
Influence of Principal Quantum Number on Energy
Electrons in higher principal quantum levels possess more energy. This energy difference is crucial in quantum mechanics, affecting phenomena like photon absorption and emission.
Azimuthal Quantum Number’s Role in Orbital Shape
The azimuthal quantum number fine-tunes our understanding by delineating the shape of orbitals. These shapes are not just academic; they dictate how atoms connect with each other, forming the basis of molecular structure and chemistry.
Quantum Number Values
Understanding the allowed values for �n and �l is fundamental.
Allowed Values for Principal and Azimuthal Quantum Numbers
- Principal Quantum Number (�n): Positive integers (1, 2, 3, …)
- Azimuthal Quantum Number (�l): Integer values from 0 to �−1n−1
Calculation and Examples
- For �=2n=2, �l can be 0 or 1, indicating s and p orbitals.
- If �=3n=3, �l can be 0, 1, or 2, signifying s, p, and d orbitals.
Physical Implications
The values of �n and �l have tangible effects on how electrons behave and how atoms interact with each other and with light.
How Each Quantum Number Affects Electron Behavior
- Principal Quantum Number (�n): Affects energy level and distance from the nucleus.
- Azimuthal Quantum Number (�l): Influences the shape of orbitals, impacting angular momentum and electron distribution.
Comparison Table
A quick glance at the differences between the principal quantum number (�n) and the azimuthal quantum number (�l):
| Feature | Principal Quantum Number (�n) | Azimuthal Quantum Number (�l) |
|---|---|---|
| Definition | Identifies the energy level of an electron. | Specifies the shape of an electron’s orbital. |
| Symbol | �n | �l |
| Values | Positive integers (1, 2, 3, …) | Integer values from 0 to �−1n−1 |
| Influences | Energy level and distance from the nucleus. | Shape of orbitals and angular momentum. |
| Physical Impact | Determines atom’s size and electron energy. | Influences chemical bonding and orbital orientation. |
| Observations | Affects spectral lines’ positions. | Affects spectral lines’ shapes and intensities. |
This table serves as a quick reference to understand the fundamental differences between �n and �l at a glance.
Practical Implications
In Spectroscopy
Role in Identifying Elements
Quantum numbers, especially �n and �l, are invaluable in spectroscopy, a technique that examines the interaction between matter and electromagnetic radiation. Here’s how they play a crucial role:
- Determining Energy Levels: The principal quantum number (�n) directly impacts the energy levels of electrons. In spectroscopy, this allows scientists to identify elements based on their unique energy level transitions, as each element has a distinct spectral fingerprint.
- Orbital Shapes and Spectral Lines: The azimuthal quantum number (�l) defines the shape of the electron orbitals. These shapes influence the types of transitions that can occur, affecting the intensity and shape of spectral lines observed in a spectrum.
Impact on Spectral Lines
- Energy Transitions: Electrons moving between levels with different �n values absorb or emit photons, creating spectral lines. The position of these lines helps identify the element.
- Line Shape and Intensity: The value of �l affects the shape of the orbital, and thus the probability of finding an electron in a particular region. This probability influences the intensity and shape of the spectral lines, offering clues about the electronic structure of the atom.
In Chemical Bonding
Influence on Bond Formation
The shape of electron orbitals, dictated by the azimuthal quantum number (�l), plays a pivotal role in chemical bonding:
- Orbital Overlap: The effectiveness of orbital overlap during bond formation is determined by the orbital shapes. �s orbitals (when �=0l=0) are spherical, making them symmetric around the nucleus, while �p orbitals (when �=1l=1) are dumbbell-shaped, directing the bond formation in specific directions.
- Bond Type: The type of chemical bond (covalent, ionic, or metallic) depends on the interaction between electron orbitals, which is influenced by �n and �l.
Determination of Molecular Geometry
- Orbital Hybridization: The concept of hybrid orbitals arises from the combination of different types of orbitals (s, p, d) within an atom to form bonds. The azimuthal quantum number (�l) is key in determining which orbitals can mix and the resulting geometry of molecules.
- Geometry and Reactivity: The geometry of a molecule, defined by the spatial arrangement of atoms, directly influences its reactivity and properties. Understanding �l provides insights into molecular shapes, predicting how molecules interact and react with each other.
In Quantum Computing
Potential Applications of Understanding Quantum Numbers
Quantum numbers are not just fundamental to understanding the microscopic world; they also have practical applications in the emerging field of quantum computing:
- Quantum Bits (Qubits): In quantum computing, qubits are the basic units of information, analogous to bits in classical computing. The principles of quantum numbers, particularly �n and �l, could help define the properties of qubits, influencing their stability and how they interact.
- Quantum Gates and Algorithms: Understanding the behavior of electrons through quantum numbers enables the design of quantum gates and algorithms. These quantum numbers can dictate how qubits are manipulated to perform computations, impacting the efficiency and capability of quantum computers.
- Material Science: The knowledge of quantum numbers aids in designing materials with specific electronic properties, which is crucial for developing qubits and other components of quantum computers.
FAQs
How do quantum numbers affect chemical properties?
Quantum numbers dictate the distribution and energy of electrons in an atom, which in turn influence its chemical properties. The principal quantum number (�n) defines the shell or energy level, affecting the atom’s size and the energy required for an electron to transition between levels. The azimuthal quantum number (�l) determines the shape of orbitals, influencing how atoms bond and their reactivity. Understanding these numbers allows chemists to predict molecular structure and behavior in reactions.
Can quantum numbers predict magnetic properties?
Yes, quantum numbers, particularly the azimuthal (�l) and magnetic (��ml) quantum numbers, play a crucial role in determining an atom’s magnetic properties. The azimuthal quantum number defines the shape of electron orbitals, which affects the distribution of electrons and their spin. This, along with the magnetic quantum number, which specifies the orbital’s orientation in space, contributes to the magnetic moments of atoms and molecules, influencing their magnetic properties.
What is the significance of the azimuthal quantum number in spectroscopy?
The azimuthal quantum number is pivotal in spectroscopy as it influences the shape of electron orbitals and, by extension, the energy transitions that occur during spectral emissions. Different orbital shapes result in unique energy levels for electrons. When electrons move between these levels, they absorb or emit light at specific wavelengths, producing distinct spectral lines. Spectroscopists use these lines to identify elements and analyze chemical compositions, making the azimuthal quantum number a fundamental tool in spectroscopic analysis.
Conclusion
Quantum numbers serve as the cornerstone of quantum mechanics, offering a detailed map of an electron’s journey within the atom. The principal and azimuthal quantum numbers, each with its specific role, together unravel the complex behavior of electrons. They not only facilitate a deeper understanding of the atomic and molecular worlds but also empower scientists and engineers to manipulate matter at the most fundamental level, fostering advancements in technology, medicine, and materials science.
Reflecting on their significance, it becomes clear that these quantum numbers are not just abstract concepts but the keys to unlocking the mysteries of the physical universe. They guide researchers in predicting how atoms interact, bond, and transform, paving the way for innovations that continue to shape our understanding of chemistry and physics.