Extrema in calculus represent the peaks and valleys of a function, pinpointing where it reaches its highest or lowest values. These points are crucial for understanding the behavior of functions, offering insights into their overall trends and potential applications in various fields. Extrema are classified into two main types: absolute and relative, each serving a specific purpose in mathematical analysis and real-world problem-solving.
The difference between absolute and relative extrema lies in their scope and identification. Absolute extrema refer to the highest or lowest point over the entire domain of a function, whereas relative extrema are those highs and lows observed within a particular interval of the function’s domain. This distinction is fundamental for accurately analyzing and applying mathematical models in practical scenarios.
Discussing absolute and relative extrema illuminates the intricacies of calculus and its applications. By identifying these points, mathematicians and scientists can optimize functions, predict trends, and solve complex problems across various disciplines. The exploration of these concepts not only enhances our understanding of mathematical theories but also opens up avenues for innovation and efficiency in technological, economic, and scientific endeavors.
Key Concepts Defined
Extrema Basics
Definition of Extrema
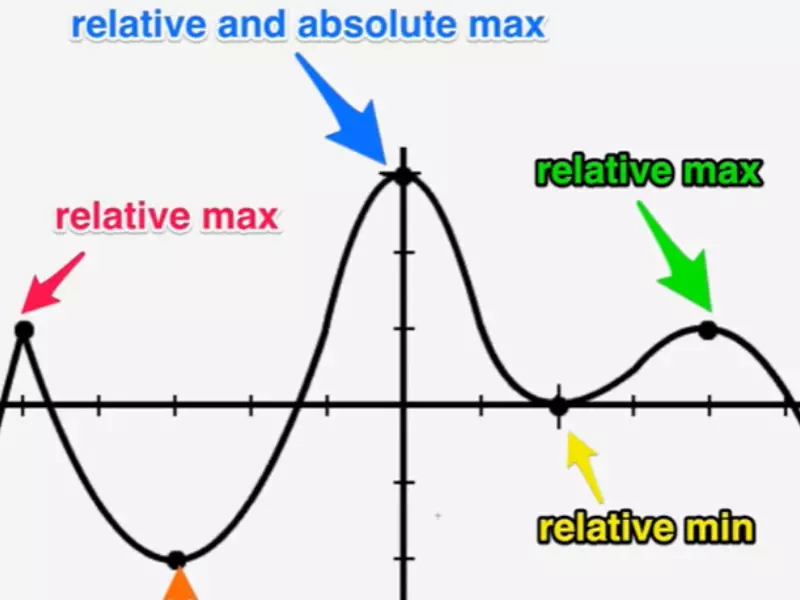
In the realm of calculus, extrema refer to the points on a graph where a function reaches its highest or lowest value. These points are crucial for understanding the overall behavior of the function. Extrema are divided into two categories: absolute and relative.
Role in Mathematical Analysis
Extrema play a pivotal role in mathematical analysis. They are used to identify the maximum and minimum values that a function can attain, which is essential in optimizing solutions in various fields such as engineering, economics, and physics.
Absolute Extrema
Definition and Characteristics
Absolute extrema are the highest or lowest points of a function across its entire domain. An absolute maximum is the highest point, while an absolute minimum is the lowest. These points represent the extreme values a function can achieve.
Finding Absolute Extrema
Finding absolute extrema involves several steps:
- Identify the domain of the function.
- Calculate the derivative of the function to find critical points.
- Evaluate the function at critical points and the boundaries of its domain.
- Compare the values to determine the highest and lowest points.
Real-world Examples
- Engineering: Determining the maximum load a bridge can support.
- Business: Finding the minimum cost to maximize profit.
Relative Extrema
Definition and Characteristics
Relative extrema are the points where a function reaches a local maximum or minimum within a specific range. A relative maximum is higher than the points directly surrounding it, and a relative minimum is lower than its immediate neighbors.
Finding Relative Extrema
To find relative extrema, follow these steps:
- Calculate the derivative of the function to locate potential extrema.
- Apply the First Derivative Test to identify if these points are relative maxima, minima, or neither.
- Evaluate the function at these points to determine their values.
Real-world Examples
- Physics: Identifying points of maximum and minimum velocity in motion.
- Economics: Analyzing local peaks and troughs in stock market trends.
Comparing Absolute and Relative Extrema
Key Differences
The key difference between absolute and relative extrema is their scope. Absolute extrema reflect the global highs and lows of a function, while relative extrema indicate local maxima and minima within a given range.
Conceptual Distinctions
- Absolute extrema are singular per domain, representing the ultimate limits of a function.
- Relative extrema can occur multiple times within the same domain, highlighting local variations.
Application Scenarios
- Optimization problems often seek absolute extrema to find the best possible outcome.
- Pattern analysis in data might focus on relative extrema to understand local trends and behaviors.
Visualization Techniques
Graphical Representation
Graphs are a powerful tool for visualizing functions and their extrema. They help illustrate the concept of highs and lows, making it easier to identify absolute and relative extrema visually.
Identifying Extrema on Graphs
- Absolute extrema appear as the highest or lowest points on the entire graph.
- Relative extrema are seen as peaks or valleys within a specific portion of the graph.
Mathematical Approaches
Calculating Absolute Extrema
Closed Interval Method
The closed interval method is a systematic approach to find absolute extrema:
- Define the interval where the function is continuous.
- Calculate the function’s values at critical points and endpoints.
- Identify the maximum and minimum values from these points.
Critical Points Evaluation
Evaluating critical points involves:
- Finding the derivative of the function.
- Solving for where the derivative is zero or undefined.
- Checking these points against the function’s domain.
Calculating Relative Extrema
First Derivative Test
The first derivative test determines if a critical point is a relative maximum or minimum:
- Calculate the derivative of the function.
- Test the sign of the derivative before and after each critical point.
- Identify the nature of the extrema based on the change in sign.
Second Derivative Test
The second derivative test provides another way to identify relative extrema:
- Find the second derivative of the function.
- Plug in the critical points into the second derivative.
- Determine the concavity at these points to classify the extrema.
Practical Applications
In Science and Engineering
Application in Physics
The principles of extrema are fundamental in physics, where they are used to solve a wide array of problems, from determining the optimal conditions for a physical system to analyzing the points of equilibrium. For instance, in mechanics, the concept of potential energy minima is used to find stable equilibrium positions. Similarly, in optics, extrema principles help design lenses and mirrors that minimize distortion and maximize focus.
Application in Engineering
In engineering, extrema are employed to optimize designs and processes. This can involve maximizing the efficiency of a system or minimizing the materials used without compromising on strength. For example, in structural engineering, the analysis of stress and strain curves allows for identifying the maximum load a structure can bear. In electrical engineering, extrema are used to optimize signal processing, reducing noise and improving clarity.
In Economics and Finance
Maximizing Profit
Extrema play a crucial role in economics by helping businesses determine the price points that maximize profits. This involves analyzing cost functions and revenue functions to find the point where the difference (profit) is at its maximum. Such analysis often involves calculus, particularly the use of derivatives to find critical points where the profit function reaches its maximum value.
Minimizing Cost
Similarly, businesses and economies aim to minimize costs while maintaining or improving the quality of services or products. Extrema are used to identify the most efficient allocation of resources, such as labor and capital, to achieve the lowest possible cost of production. This involves calculating the cost function’s minima, again relying heavily on the concepts of derivatives and critical point analysis.
Challenges and Solutions
Common Challenges
Identifying Extrema in Complex Functions
One significant challenge is the identification of extrema in complex functions, particularly those with multiple variables or those that are not easily differentiable. These functions can have a vast number of local maxima and minima, making it difficult to determine the global extrema.
Misinterpretation of Extrema
Another challenge is the misinterpretation of extrema, especially when analyzing real-world data. Noise and outliers can often lead to incorrect identification of critical points, resulting in flawed decision-making.
Strategies for Overcoming Challenges
Analytical Methods
Analytical methods involve a deeper understanding of the function and its derivatives. This includes:
- Enhanced Critical Point Analysis: Beyond just finding where the derivative equals zero, this involves understanding the behavior of the function around these points.
- Use of Higher Derivatives: Applying tests like the second derivative test to confirm the nature of the extrema and ensure that they are not points of inflection.
Computational Tools
Computational tools have become indispensable in overcoming the challenges of identifying and analyzing extrema, especially in complex and high-dimensional problems. These tools include:
- Software Programs: Mathematical and statistical software like MATLAB, Mathematica, and R, which can handle complex calculations and visualize functions, making it easier to identify extrema.
- Optimization Algorithms: Techniques like gradient descent, simulated annealing, or genetic algorithms that can efficiently search for global maxima or minima in complex landscapes.
By leveraging both analytical methods and computational tools, professionals in various fields can effectively tackle the challenges associated with finding and interpreting extrema. This dual approach enables a deeper understanding of the problems at hand and allows for more accurate and reliable solutions.
Frequently Asked Questions
How do you find absolute extrema?
To find the absolute extrema of a function, you must examine the function’s values at critical points and endpoints within its domain. First, determine the derivative of the function and find where it equals zero or is undefined to identify critical points. Then, evaluate the function at these points and its domain boundaries. The highest and lowest values among these are the absolute maximum and minimum, respectively.
Can a function have more than one relative extrema?
Yes, a function can have multiple relative extrema. These occur at points where the function’s slope changes from positive to negative (relative maximum) or negative to positive (relative minimum). The existence of multiple relative extrema depends on the function’s nature and complexity, showcasing the varying trends and turning points within a specific domain.
Why are extrema important in real life?
Extrema play a crucial role in real life by enabling the optimization of processes and decision-making in various fields. For example, in engineering, finding the maximum stress a material can withstand helps in designing safer structures. In economics, determining the minimum cost of production can lead to more efficient budget management. Thus, identifying extrema helps in maximizing efficiency, safety, and profitability in practical applications.
Conclusion
Understanding the differences between absolute and relative extrema enriches our comprehension of calculus and its practical implications. This knowledge allows for the optimization of functions and the effective resolution of complex problems in science, engineering, and economics. By mastering the identification and application of extrema, individuals can unlock new potential in technological advancements and strategic decision-making.
The exploration of absolute and relative extrema underscores the beauty and utility of mathematics in the real world. It demonstrates how theoretical concepts can be applied to solve real-life challenges, highlighting the importance of mathematics in driving innovation and improving our understanding of the universe.
