Mathematics, with its complex web of concepts, symbols, and operations, serves as the bedrock for logical reasoning and analytical thinking. Among its diverse components, the notions of relations and functions stand out as fundamental to understanding the mathematical landscape. These concepts not only provide the framework for mathematical analysis but also find applications across various scientific disciplines, making their distinction crucial for students and professionals alike.
A relation in mathematics is a connection between sets of information, where each member of one set is associated with one or more members of another set. A function, on the other hand, is a special type of relation where every element in the first set is associated with exactly one element in the second set. This distinction underscores the uniqueness of functions within the broader category of relations, highlighting their importance in both theoretical and applied mathematics.
The study of relations and functions extends beyond the identification of these connections; it encompasses the exploration of their properties, types, and applications. By examining how relations can evolve into functions under specific conditions, and how these mathematical structures can be visualized and applied, we gain deeper insights into the systematic organization of data and the predictive capabilities of mathematical models.
Basic Definitions
Relation: Definition and Examples
A relation in mathematics represents a connection between elements of two sets. Think of it as a way to link or relate items from one group to another. For example, in a classroom setting, a relation could describe the pairing of students (set A) with their chosen subjects (set B). This relation doesn’t insist on exclusivity; a student might be linked to several subjects, illustrating the flexibility of relations in connecting elements.
Function: Definition and Examples
Moving to functions, these are a specific type of relation with a stricter rule: every element in the first set (domain) is connected to exactly one element in the second set (range). A classic example of a function is the relationship between hours worked and wages earned. If you work for a fixed hourly rate, your total earnings can be uniquely determined by the number of hours you’ve worked, embodying the essence of a function’s singular mapping.
Key Characteristics
Relation Characteristics
Domain and Range
The domain and range are foundational concepts in discussing relations. The domain refers to the set of all possible inputs, while the range encompasses all possible outputs. For instance, in a relation describing a book club’s members and their favorite genres, the domain is the members, and the range includes the genres they prefer.
Examples in Real Life
Relations surface in various real-life scenarios. A business’s relation between its products and their prices is a simple yet profound example, demonstrating how multiple products can share the same price point.
Function Characteristics
Unique Output for Each Input
Functions are characterized by their requirement for a unique output for each input, ensuring a one-to-one or many-to-one relationship between the domain and range. This characteristic guarantees predictability and precision in functions, contrasting with the broader possibilities in relations.
Function Notation and Examples
Function notation, often expressed as f(x), simplifies conveying the relationship between input (x) and output. For instance, if f(x) = x^2, this function squares any input value, mapping each number to a unique output.
Types of Relations
Reflexive, Symmetric, and Transitive
Relations can be classified as reflexive, symmetric, and transitive, each with distinct features. A reflexive relation means every element relates to itself, like a person being the same age as themselves. Symmetric relations imply that if A is related to B, then B is related to A, akin to mutual friendships. Transitive relations suggest that if A is related to B, and B is related to C, then A is directly related to C, mirroring social networks’ connections.
Equivalence Relation
An equivalence relation combines all three characteristics (reflexive, symmetric, transitive), partitioning a set into equivalence classes. This concept finds practical application in sorting algorithms and classification tasks in computer science, where objects are grouped based on shared attributes.
Types of Functions
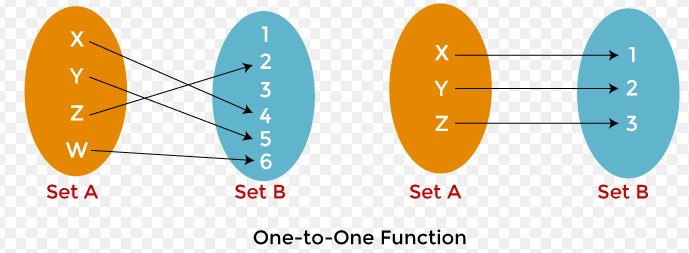
One-to-One (Injective)
A function is one-to-one (injective) if each element of the domain maps to a unique element in the range. A real-world example is assigning each student a unique ID number, ensuring no two students share the same ID.
Onto (Surjective)
An onto (surjective) function means the range includes every possible value at least once. In practical terms, this could resemble a situation where every job role in a company is filled.
Bijective
Combining both concepts, a bijective function is both injective and surjective, meaning it’s a one-to-one match between all elements of the domain and range. This ideal scenario finds applications in cryptographic algorithms where unique keys map to unique messages.
Visualizing Differences
Graphical Representation
Graphs offer a visual means to distinguish between relations and functions. In a graph, a function will pass the vertical line test, where no vertical line intersects the graph more than once. This visual tool elucidates the function’s unique mapping principle.
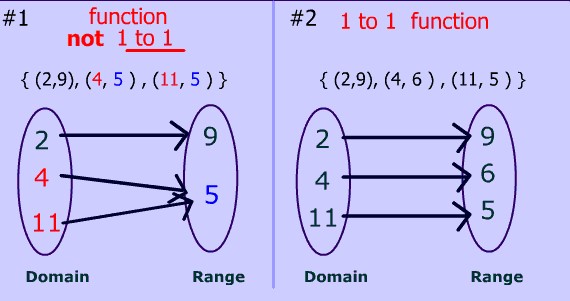
Mapping Diagrams
Mapping diagrams further clarify the distinction, illustrating how each element of a function’s domain corresponds to one element in the range. Conversely, relations might show multiple connections emanating from a single domain element, visually capturing the essence of their difference.

Mathematical Formulation
Set Theory Perspective
In set theory, both relations and functions serve as fundamental concepts for understanding the relationships between elements of different sets. A relation is essentially a subset of a Cartesian product of two or more sets. This means if we have sets A and B, any pair (a, b) where a is in A and b is in B, and which satisfies a certain condition, is part of the relation.
Functions are a special type of relation with a unique characteristic: every element of set A (the domain) is associated with exactly one element of set B (the codomain). This unique pairing is what distinguishes functions from general relations.
Algebraic Approach
From an algebraic perspective, relations and functions can be expressed through equations. For relations, an equation like y = 2x + 3 doesn’t necessarily define a function on its own; it depends on the sets of values chosen for x and y. However, if every x-value is paired with exactly one y-value, this equation then represents a function.
Functions can further be categorized based on their algebraic properties. For example, linear functions have the form f(x) = mx + b, where m and b are constants. This algebraic approach helps in understanding how functions behave and how they can be graphed.
Practical Applications
In Computer Science
In computer science, functions are a cornerstone. They allow programmers to encapsulate code blocks that perform specific tasks and return results. This not only makes programs more readable and maintainable but also facilitates code reuse. Functions in programming often take inputs, process them, and return an output, mirroring the mathematical definition of functions.
In Everyday Life
The concepts of relations and functions are not confined to the realm of mathematics and computer science; they play a crucial role in everyday decisions. For example, determining the cost of fuel for a trip involves a function where the distance of the trip is an input, and the cost is the output. Similarly, cooking recipes can be seen as functions where the inputs are ingredients, and the output is the finished dish.
Common Confusions
Not All Relations Are Functions
A common point of confusion arises when distinguishing between relations and functions. It’s crucial to remember that not all relations are functions. A relation that assigns more than one output to a single input is not a function. Understanding this distinction helps in correctly categorizing mathematical relationships.
Misinterpretations of Graphs
Graphs are a powerful tool for visualizing relations and functions. However, misinterpretations of graphs can lead to incorrect conclusions. A common mistake is assuming that a graph represents a function without applying the vertical line test, which checks if any vertical line would intersect the graph more than once. If it does, the graph does not represent a function.
Learning and Teaching Tips
Strategies for Understanding
Effective strategies for understanding relations and functions involve visual aids like graphs and mapping diagrams, which can help conceptualize how inputs are related to outputs. Another strategy is to use real-life scenarios to illustrate these concepts, making them more relatable and easier to grasp.
Tips for Students and Educators
For students, practicing with diverse problems and using online tools to visualize concepts can be incredibly beneficial. For educators, it’s important to present these concepts in a step-by-step manner, ensuring students understand the foundation before moving on to more complex topics. Incorporating interactive elements into lessons can also enhance understanding and engagement.
Interactive Resources
Several online tools and software offer interactive experiences for exploring relations and functions. Websites like Desmos allow users to graph functions and relations, providing immediate visual feedback. Educational platforms like Khan Academy offer exercises and video tutorials that cover these concepts in depth, making learning more accessible and engaging.

FAQs
What defines a function in mathematics?
A function is defined by its unique characteristic that associates each element in its domain (the set of all possible inputs) with exactly one element in its range (the set of all possible outputs). This relationship ensures that for every input there is a single, well-defined output, distinguishing functions from general relations where multiple outputs for a single input can exist.
How can a relation fail to be a function?
A relation fails to be a function when an element in the domain is associated with more than one element in the range. In other words, if there are two or more possible outputs for a single input, the relation does not meet the strict criterion required for a function, which demands one-to-one correspondence between inputs and outputs.
What are some examples of functions in real life?
Functions manifest in various real-life scenarios, such as calculating the speed of a moving object (where speed is a function of distance over time), determining the total cost of items purchased (where cost is a function of the number of items and their individual prices), and predicting weather patterns (where the forecast can be seen as a function of temperature, humidity, and other atmospheric conditions).
How are functions used in computer science?
In computer science, functions play a crucial role in structuring code efficiently and logically. They are used to perform specific tasks or calculations based on inputs, returning outputs without altering the state of the system. Functions facilitate code reusability, modularity, and abstraction, making complex programming tasks more manageable and understandable.
Conclusion
The concepts of relations and functions constitute the cornerstone of mathematical analysis, providing a systematic approach to understanding and organizing data. The distinction between these two entities not only clarifies the structure of mathematical relationships but also enhances our capacity to model and solve real-world problems. By grasping the essence of functions as relations with unique outputs for each input, we unlock the potential to apply mathematical principles more effectively in various fields.
Understanding and differentiating between relations and functions is more than an academic exercise; it is a fundamental skill that underpins logical reasoning and analytical thinking. As we continue to explore the vastness of mathematics and its applications, the knowledge of how to distinguish and utilize these concepts becomes invaluable, empowering us to solve complex problems and innovate within and beyond the realm of mathematics.