The relationship between variance and covariance is one of the most important concepts in statistics, and it’s essential for understanding how different variables interact. In this blog post, we’ll take a closer look at variance and covariance, and discuss their implications for data analysis.
Finally, we’ll explore some practical applications of variance and covariance in data science.
Definition of variance and covariance
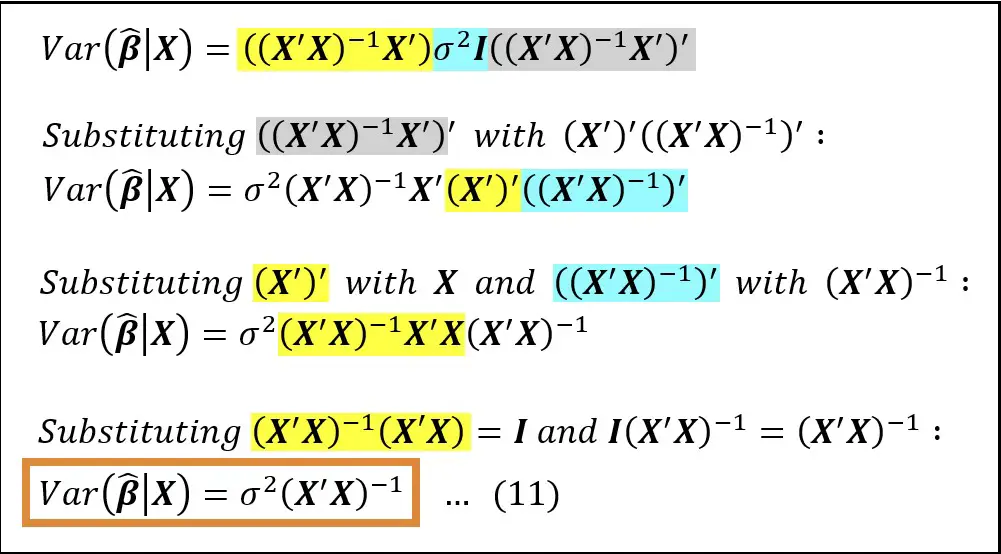
Variance and covariance are two important concepts in mathematics and statistics that describe the relationship between two sets of data. Variance is a measure of the spread of individual values in a dataset, while covariance is a measure of how two variables vary together. Variance and covariance are used to quantify how much two variables are related to each other.
For example, if one variable increases, how does the other variable change? If they increase together, then the covariance is positive; if one decreases while the other increases, the covariance is negative.
Understanding the variance and covariance of a dataset can help you make predictions about future data points.
Applications of variance and covariance
Variance and covariance are two closely related concepts in statistics that measure the relationship between two variables. Variance measures the degree of spread in a data set, while covariance measures the degree of linear association between two variables.
Both of these measures are used to gain insights into the relationship between two variables, which can be used in a variety of applications. For example, variance and covariance can be used to identify correlations between stock prices and economic indicators, predict future stock prices, and understand the risks associated with certain investments. Additionally, the relationship between variance and covariance is an important tool in portfolio management, as it can be used to determine the optimal combination of investments to maximize returns.
Common misconceptions about variance and covariance
When it comes to understanding the relation between variance and covariance, it is important to realize that they are not interchangeable. While both terms measure the degree to which two variables are related, variance describes the variability of a single variable while covariance describes the joint variability of two variables.
In other words, covariance measures the relationship between two variables, while variance measures the variability of one variable.
Examples of variance and covariance in practice
Variance and covariance are two closely related concepts in statistics that measure how two random variables change together. Variance measures how much a single variable deviates from its average, while covariance measures the degree to which two variables move together.
For example, if you observe a high covariance between two variables, it may indicate that changes in one variable will cause changes in the other. On the other hand, a low covariance might suggest that the two variables are relatively independent of each other.
In addition, if the variance of one variable is high, it might suggest that the data is spread out and the average value is not a good representation of the data.
How to calculate variance and covariance

Variance and covariance are two important metrics in statistics that measure the relationship between two variables. Variance is a measure of how much one variable deviates from its mean, while covariance is a measure of how two variables are related to each other.
By calculating variance and covariance, we can gain insight into how variables are related to each other, and how changes in one variable can affect the other. Knowing how to calculate variance and covariance can help us make more informed decisions about how to best manage our data.
Conclusion
In conclusion, variance and covariance are closely related concepts in statistics. Variance measures the spread of a single variable, while covariance measures the relationship between two variables.
The magnitude of the covariance is determined by the variance of both variables, with higher variances leading to higher covariances. Therefore, it is important to understand the relation between variance and covariance in order to make sound statistical decisions.

