When it comes to geometry, understanding the relation between perimeter and area can help to solve a variety of problems. In this blog post, we will explore the connection between perimeter and area and discuss how they can be used to calculate the area of shapes. By the end of this blog, you should have a better understanding of how the two measurements interact with each other and how to calculate the area of shapes.
Understanding the basics of perimeter and area

When it comes to geometry, understanding the relationship between perimeter and area is essential. Perimeter is the total length of the boundary of a two-dimensional shape.
On the other hand, area is the measure of the size of a shape’s interior. It is calculated by multiplying the length and width of a shape. A simple example is a rectangle: its perimeter is the sum of the lengths of all four sides while the area is the product of its length and width.
The fundamental relationship between perimeter and area is that as the perimeter of a shape increases, the area of the shape increases as well. Therefore, if you double the perimeter of a shape, the area of the shape will also double. This is because when the perimeter increases, the length and width of the shape also increase, and so does the area.
Calculating the area of a regular polygon using perimeter
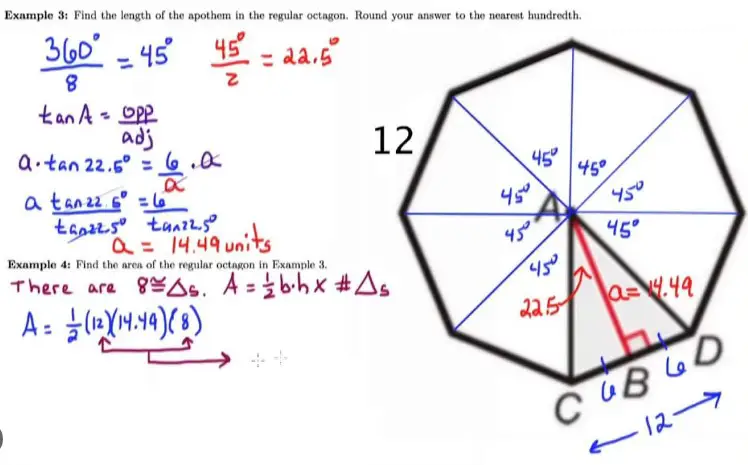
The relationship between the perimeter and area of a regular polygon is simple yet powerful. A regular polygon is a closed shape with equal length sides and equal angles between them. By using the perimeter of the polygon, we can calculate its area.
The formula for this calculation is simple: Area = (perimeter x apothem) / The apothem is the distance from the center of the polygon to one of its sides.
Knowing the perimeter and the apothem of a regular polygon, it is easy to calculate its area. This relationship between perimeter and area can be used to great effect in solving complex geometry problems quickly and accurately.
Applying the relationship between perimeter and area to irregular shapes
The relationship between perimeter and area of a shape is an important concept in geometry. When it comes to irregular shapes, it’s a bit more challenging to calculate the area and perimeter. However, by understanding the basic principles behind this relationship, it can still be applied to irregular shapes.
By breaking down the shape into regular shapes, it is possible to calculate the area and perimeter of each of the regular shapes, and then add them together to get the total area and perimeter of the irregular shape. This technique can be applied to any type of irregular shape, allowing us to better understand the relationship between perimeter and area in a more meaningful way.
How to use the relationship to find the area of a rectangle
The relationship between the perimeter and area of a rectangle is one that is often overlooked, but can be incredibly useful in determining the area of a rectangle. Perimeter is defined as the total length of the sides of a shape, while area is the amount of space inside a shape. Knowing this, you can easily use the relationship between perimeter and area to calculate the area of any rectangle.
Knowing this, you can easily use the relationship between perimeter and area to calculate the area of any rectangle. For example, if a rectangle has a perimeter of 12, you can divide 12 by 4 (the number of sides of the rectangle) to get the length of each side, which would be Then, you can use the length of each side to calculate the area by multiplying the length by the width.
In this case, the area of the rectangle would be Knowing the relationship between perimeter and area of a rectangle can be a great tool for quickly and accurately calculating the area of any rectangle.
Examples of how to use this relationship to solve complex problems
The relationship between perimeter and area can be a powerful tool for solving complex problems. For instance, when dealing with a rectangle, the area can be determined by multiplying the length of two adjacent sides, while the perimeter is calculated by adding the lengths of all four sides.
By understanding the relationship between these two components, we can easily solve problems like calculating the length or width of a rectangle given the area or perimeter. This simple relationship can be used to solve more complex problems such as finding the area of a triangle or creating a hexagon given specific measurements. By understanding the relationship between perimeter and area, we can unlock a wide range of problem-solving possibilities.
Final Touch
In conclusion, the relation between the perimeter and area of a shape is dependent on the shape itself. For example, a circle has a constant ratio of circumference to area, while a square has a constant ratio of side length to area. The perimeter and area of a shape can also change depending on the size of the shape, with the ratio of the perimeter to area remaining the same.
With this knowledge, it is possible to calculate the area or perimeter of a shape by knowing the other, given the shape and size of the shape.

