It is common to come across various statistical terms in everyday life. Mean, median and mode are three terms that are often used in conjunction with one another.
How to calculate mean, median and mode
To understand the relationship between mean, median and mode, it’s important to first understand what each of them represent. The mean, also known as the average, is the sum of all of the values in a set divided by the number of values in the set.
The median is the middle value when all of the values in a set are arranged in ascending order. Lastly, the mode is the value that appears most often in the set. It’s easy to see how these three measures of central tendency are related.
If the data set contains the same value for each item, the mean, median and mode will all be the same. However, if the values in the set vary, the mean, median and mode can be very different.
5 and the mode is As you can see, the mean, median and mode can vary greatly, even in a small sample size.
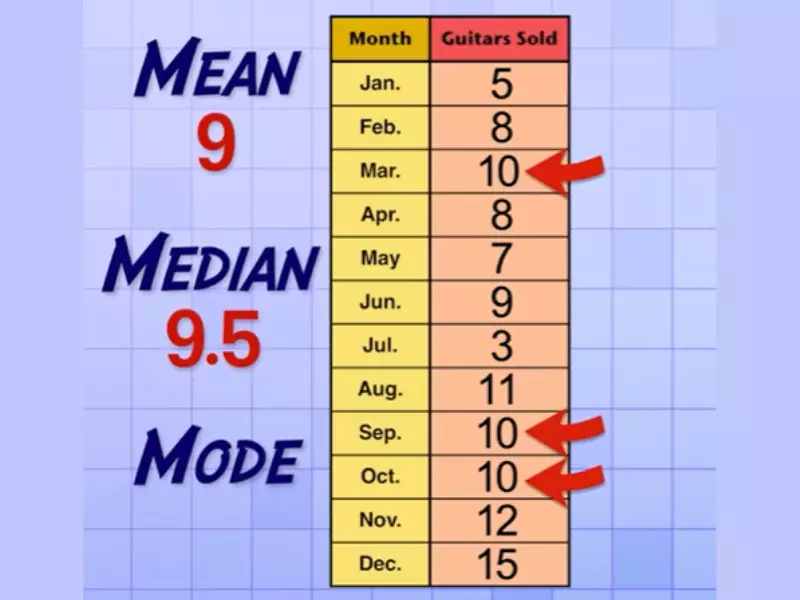
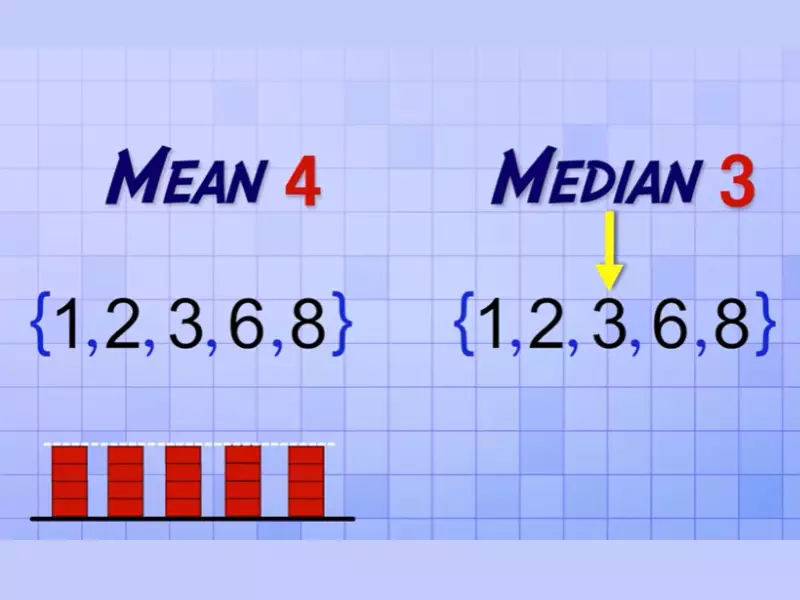
Examples of mean, median and mode calculations
The terms mean, median and mode are often used when discussing data sets and the results of statistical analyses. Mean, median and mode are all ways to measure the center of a data set.
The mean is the average of all the values in a data set, the median is the middle value and the mode is the most frequent value. Understanding the differences between these three measures can help us understand the data set better and draw more meaningful conclusions from it. While the mean is the most commonly used measure of center, the median and mode can be used to gain additional insight into the data set.
For example, if the mean and median of a data set are the same, it indicates that the data is symmetrically distributed. If the mode is much higher or lower than the mean and median, it indicates that the data is skewed.
Understanding the differences between mean, median and mode
Understanding the relationship between mean, median and mode can be tricky. But once you understand the differences, it can help you better analyze data and draw conclusions.
Mean is the average of a set of numbers. It is calculated by adding up all the values and then dividing by the total number of values. Median is the middle number in a set of values when they are arranged in numerical order.
Mode is the most frequently occurring value in a set of data. All three measures can be used to describe the center of a data set, but which one is best depends on the type of data you are working with.
Knowing the differences between mean, median and mode can help you better understand and analyze your data.
Benefits of knowing the relation between mean median and mode
Understanding the relationship between mean, median, and mode is essential for any data analyst. Knowing these basic concepts can help you to make more informed decisions when interpreting numerical data, and can help you to better understand the underlying patterns contained within.
The mean, median, and mode are three important measures of central tendency that provide a summary of the distribution of a dataset. The mean is the average, the median is the middle value in a dataset, and the mode is the most frequent value. Each of these measures of central tendency can provide unique insights into the data and can be used to draw different conclusions.
By recognizing the differences between mean, median, and mode, you can gain a better understanding of the data and the underlying patterns it contains.
Common pitfalls in interpreting mean, median and mode
Understanding the differences between the mean, median, and mode is essential in interpreting data correctly. The mean, median and mode are all measures of central tendency.
The mean is the arithmetic average of a set of values, calculated by adding up all of the values and dividing by the number of values. The median is the middle value when values are arranged in either numerical or alphabetical order.
The mode is the value which appears most frequently in a set of values. It is important to be aware of the potential pitfalls when interpreting these measures. For example, the mean is heavily influenced by outliers, while the median is not.
Also, if the data set includes multiple modes, the mode is not useful for describing the central tendency. Lastly, if the data includes no repetitions, the mode does not exist.
Being aware of these common pitfalls will help you interpret data correctly.
Tips for analyzing data with mean, median and mode
If you are looking to analyze data, it’s important to understand the relationship between mean, median and mode. Mean is the average for a set of numbers, while median is the middle value of a set of numbers.
All three of these can be used to gain valuable insights into your data. By understanding the relationship between mean, median and mode, you can start to build a more complete picture of your data.
Additionally, knowing how these three values interact can help you identify trends or outliers that might otherwise go unnoticed. Ultimately, understanding the relationship between mean, median and mode can be a great way to get a better understanding of the data you are working with.
Final Touch
In conclusion, the mean, median, and mode are all measures of central tendency that can be used to describe the center of a dataset. However, they are calculated differently and can give different results. The mean is the average of all values, the median is the middle value, and the mode is the most frequent value.
The mean is affected by outliers, the median is not, and the mode can be affected if there are multiple values that are the most frequent. Therefore, it is important to consider all three measures when analyzing a dataset in order to get a full picture of the data.
