Waves permeate through nearly every aspect of our natural and technological world, from the ripples on a pond to the signals connecting our smartphones. At the heart of understanding these waves are two fundamental concepts: frequency and period. These terms are crucial in fields ranging from physics to engineering, influencing everything from the music we hear to the way we communicate.
The relationship between frequency and period is straightforward yet profound. Frequency, measured in Hertz (Hz), denotes how often a wave completes a cycle in one second. In contrast, the period, measured in seconds, represents the duration of time it takes for a wave to complete one cycle. Essentially, frequency and period are inversely related; as one increases, the other decreases.
Understanding the intricacies of this relationship opens the door to mastering wave phenomena. It lays the groundwork for deeper exploration into how waves travel, interact, and affect our world. By examining how frequency and period dictate the behavior of waves, we unlock a deeper appreciation for the natural and engineered systems that rely on these principles.
Frequency Explained
Definition
Frequency is a key concept in understanding how waves behave. It measures how often something happens over a specific time period. In the context of waves, frequency indicates the number of cycles a wave completes in one second. A cycle can be thought of as one complete wave oscillation, which might mean a crest and a trough for a water wave or a compression and rarefaction for a sound wave.
Unit of Measure
The unit of measure for frequency is the Hertz (Hz). One Hertz signifies one cycle per second. This unit honors Heinrich Hertz, a pioneer in the study of electromagnetic waves. Frequencies can range from just a few cycles per second to billions of cycles per second, known as gigahertz (GHz).
Real-world Examples
- Radio Waves: FM radio stations broadcast at frequencies around 88 to 108 MHz (megahertz), which means the electromagnetic waves they emit cycle 88 to 108 million times per second.
- Sound Waves: Middle C on a piano vibrates at about 261.6 Hz, creating sound waves that cycle 261.6 times per second.
- Light Waves: The red light has a frequency of around 430–480 THz (terahertz), cycling hundreds of trillions of times per second.
Period Explained
Definition
The period is the flip side of frequency. It measures the duration of time it takes for one cycle of a wave to occur. If you’re watching waves crash on the shore, the period is the time between successive waves hitting the beach. For a pendulum, it’s the time it takes to swing back to its original position.
Unit of Measure
The period is measured in seconds. However, depending on the context and the length of the cycle, milliseconds (ms), microseconds (µs), or even larger units like minutes might be used. The key is that the period focuses on time, specifically how much time passes during one cycle of whatever phenomenon you’re observing.
Real-world Examples
- Earth’s Rotation: The period of Earth’s rotation around its axis is 24 hours, meaning it takes a full day for one complete rotation.
- Heartbeat: A human heart might have a period of 0.8 seconds between beats at a resting rate, indicating the time from the start of one beat to the start of the next.
- Traffic Lights: A traffic light might cycle every 120 seconds, with the period of the entire red-yellow-green sequence taking two minutes.
Core Relation
Mathematical Connection
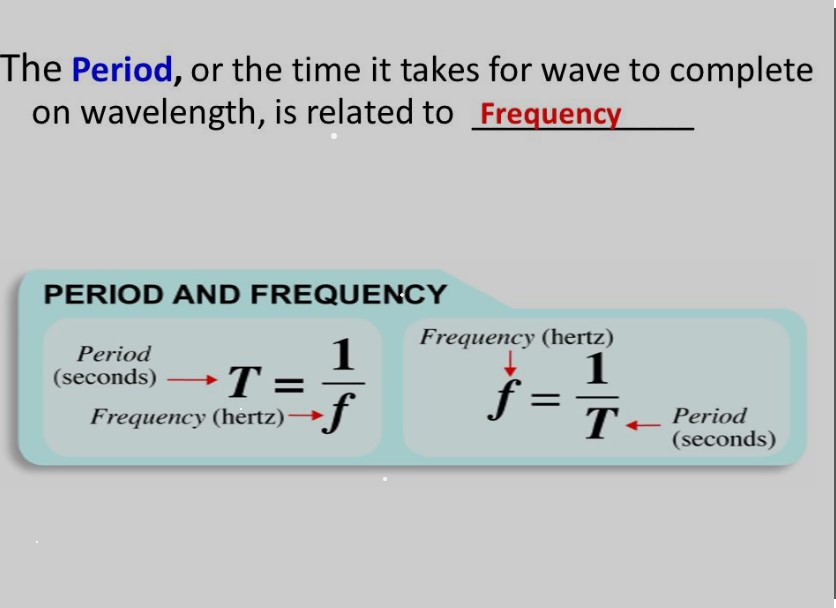
The relationship between frequency and period is mathematically inverse. When one increases, the other decreases. This is because frequency measures cycles per second, while the period measures the seconds per cycle. They are reciprocal quantities expressed by the equation:
Frequency (Hz)=1Period (s)Frequency (Hz)=Period (s)1
Formula Derivation
Deriving the formula for the relationship between frequency and period starts with their definitions. Since frequency is the number of cycles per second, and the period is the time for one cycle, it follows that:
Frequency=Number of CyclesTimeFrequency=TimeNumber of Cycles
For one cycle, this simplifies to:
Frequency=1PeriodFrequency=Period1
This equation highlights how intimately linked these two concepts are, each defining a unique aspect of wave behavior.
Calculating Frequency
Step-by-step guide
Calculating frequency when you know the period of a wave involves a simple formula:
- Step 1: Identify the period of the wave in seconds.
- Step 2: Use the formula Frequency=1PeriodFrequency=Period1.
- Step 3: Calculate the frequency by taking the reciprocal of the period.
Examples
- Pendulum Swing: If a pendulum takes 2 seconds to complete one back-and-forth swing, its period is 2 seconds. Thus, its frequency is 12=0.5��21=0.5Hz.
- Blinking Light: A light blinks on and off every 4 seconds. The period of the light’s cycle is 4 seconds, making the frequency 14=0.25��41=0.25Hz.
Calculating Period
Step-by-step guide
To determine the period of a wave when the frequency is known, follow these straightforward steps:
- Step 1: Obtain the frequency of the wave in Hertz (Hz).
- Step 2: Apply the formula Period (s)=1Frequency (Hz)Period (s)=Frequency (Hz)1.
- Step 3: Calculate the period by taking the reciprocal of the frequency.
Examples
- Radio Broadcast: An FM station broadcasting at 100 MHz (megahertz, or millions of Hertz). The frequency is 100×106��100×106Hz. The period, therefore, is 1100×106=10−8100×1061=10−8 seconds.
- Flashing Beacon: A beacon flashes light with a frequency of 2 Hz. The period is 12=0.521=0.5 seconds between flashes.
Applications
In Music
Pitch and Notes
The frequency of sound waves determines the pitch of the notes we hear. A higher frequency results in a higher pitch. Musical instruments and voices produce sounds at specific frequencies, creating notes that form melodies and harmonies. For instance, the standard tuning for middle A is 440 Hz, which serves as a reference point for tuning musical instruments.
In Electronics
Signal Processing
In electronics, frequency and period are crucial for signal processing, which involves the analysis and manipulation of electrical signals. Devices such as oscillators and filters use these concepts to produce and modify signals for various applications, from audio equipment to telecommunications systems.
In Astronomy
Orbital Periods
The period is also significant in astronomy, where it refers to the time it takes for a celestial body to complete one orbit. For example, Earth’s orbital period around the Sun is approximately 365.25 days, defining our year.
Key Differences
Summary Table
| Aspect | Frequency | Period |
|---|---|---|
| Definition | Number of cycles per second | Time taken for one complete cycle |
| Unit of Measure | Hertz (Hz) | Seconds (s) |
| In Music | Determines pitch | Rhythm and tempo |
| In Electronics | Used in signal generation and processing | Defines signal duration |
| In Astronomy | Orbital frequencies of celestial bodies | Time for one complete orbit |
Impact on Wave Properties
Frequency and period directly affect wave properties such as energy, amplitude, and speed. In light waves, for example, a higher frequency (shorter period) corresponds to higher energy and vice versa. This relationship is essential in technologies like laser physics and radio transmission.
Visual Aids
Graphs and Charts
Graphs showing the relationship between frequency and period can help visualize their inverse relationship. A plot of frequency on the x-axis and period on the y-axis would show a hyperbolic curve, indicating that as one increases, the other decreases.
Diagrams of Wave Cycles
Diagrams depicting wave cycles illustrate how the period relates to the physical space the wave occupies. A single cycle might be marked from crest to crest or trough to trough, with the distance between these points representing the wavelength, which is inversely related to frequency.
Practical Implications
Everyday Applications
Understanding frequency and period has everyday applications, such as tuning musical instruments, setting the rhythm of a song, or even in the blinking rate of LED indicators on appliances and electronic devices.
Technological and Scientific Significance
The principles of frequency and period underpin significant technological advances. In telecommunications, varying frequencies allow for the transmission of data over the airwaves. In medical technology, ultrasound devices use high-frequency sound waves to create images of internal body structures. This knowledge is not just academic; it’s applied daily in fields that impact our lives directly.
FAQs
What is frequency in simple terms?
Frequency refers to the number of complete cycles a wave undergoes in one second. It’s like counting how many times a pendulum swings back and forth within that time frame. Measured in Hertz (Hz), frequency gives us an insight into the rapidity of these oscillations, defining the speed of the wave’s vibrations.
How do you calculate the period of a wave?
To calculate the period of a wave, you take the reciprocal of the frequency. If the frequency of a wave is given in Hertz (Hz), which is cycles per second, then the period (T) is the number of seconds per cycle. The formula to find the period is T = 1/f, where ‘f’ is the frequency.
Why are frequency and period inversely related?
Frequency and period are inversely related because they are two sides of the same coin. Frequency measures how many cycles occur in a second, while period measures the time it takes for one cycle to complete. As the frequency of a wave increases, it completes more cycles in a second, reducing the time (period) each cycle takes. Conversely, a lower frequency means fewer cycles per second, resulting in a longer period for each cycle.
Can two different waves have the same frequency?
Yes, two different waves can have the same frequency but differ in other characteristics such as amplitude, phase, or waveform shape. Frequency solely describes how often the wave cycles occur, not the height or form of the wave. This is why two sounds can have the same pitch (frequency) but sound different due to other attributes like timbre or intensity.
Conclusion
The dance between frequency and period is a fundamental aspect of understanding wave behavior across various domains. By grasping this relationship, we can predict and manipulate wave properties to serve countless applications, from designing better communication systems to enhancing musical compositions. It’s a testament to the elegant simplicity underlying complex phenomena.
This exploration of frequency and period not only enriches our comprehension of the physical world but also underscores the interconnectedness of scientific principles. It demonstrates how a simple mathematical relationship can have wide-reaching implications, affecting everything from the cosmic ballet of celestial bodies to the fundamental operations of modern technology.
