Factors and multiples form the backbone of many mathematical concepts and operations, serving as fundamental building blocks in the study and application of mathematics. These terms are often introduced in early education, laying the groundwork for more complex mathematical theories and practices. Understanding the relation between factors and multiples is crucial for anyone looking to deepen their mathematical knowledge or apply it in practical situations.
The relationship between factors and multiples is straightforward yet profound. Factors of a number are integers that divide the number without leaving a remainder, while multiples of a number are produced by multiplying that number by an integer. Essentially, factors can be seen as the building blocks of a number, and multiples represent the expansion of that number through multiplication.
This interplay between factors and multiples is not just a theoretical concept; it has practical applications in various fields such as algebra, geometry, and even outside mathematics, in areas like coding and algorithm development. The ability to identify and use factors and multiples can simplify complex problems, optimize solutions, and enhance understanding of mathematical relationships.
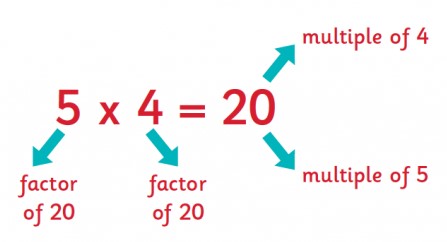
Basics of Factors
Definition and Examples
Factors are integers that you can multiply together to get another number. For instance, when we consider the number 6, its factors are 1, 2, 3, and 6 because 1×6 = 6 and 2×3 = 6. This means that both 1, 2, 3, and 6 are factors of 6. Understanding factors is crucial in mathematics because they reveal the building blocks of numbers.
Identifying Factors
Identifying the factors of a number involves finding all the whole numbers that divide evenly into that number. Here are some guidelines:
- Start with 1: Every number’s factor.
- Incrementally check numbers: Up to half the target number plus one.
- Division test: If the number divides evenly, it’s a factor.
Prime Factors
Prime factors are factors of a number that are, themselves, prime numbers. Here’s how to find them:
- Divide the number by the smallest prime number (2) and continue dividing until it can’t be divided evenly by 2.
- Move to the next smallest prime number (3), and repeat the process.
- Continue until the number cannot be divided any further.
This process breaks down a number into its prime components, which are the basic building blocks of all numbers.
Basics of Multiples
Definition and Examples
Multiples are what you get when you multiply a number by an integer. For example, the first few multiples of 5 are 5, 10, 15, 20, etc. This is because 5×1 = 5, 5×2 = 10, 5×3 = 15, and so on. Multiples continue infinitely, getting larger as you multiply by higher numbers.
Identifying Multiples
To identify multiples of a number, you simply multiply that number by the series of whole numbers:
- Start with the number itself (as every number is a multiple of itself).
- Continue multiplying by 2, 3, 4, and so on.
- This series can go on indefinitely, generating multiples.
Interrelation Explained
Direct Relationship
The relationship between factors and multiples is direct and foundational to understanding numerical relationships. Every multiple of a number incorporates its factors. For example, the factors of 4 (1, 2, and 4) are directly related to its multiples, like 8 (2×4), 12 (3×4), and so on. This shows how multiples are expansions of a number’s factors through multiplication.
Real-World Examples
Real-world applications of factors and multiples are abundant:
- Time Scheduling: Finding common meeting times within schedules.
- Tiling a Floor: Determining how many tiles fit along the lengths and widths of a room.
- Packaging Products: Calculating the arrangement of products in packaging based on factors for efficient space use.
These examples show how factors and multiples play a role in problem-solving and organization in everyday life.
Factors vs. Multiples
Key Differences
The key differences between factors and multiples are:
- Origin: Factors are numbers that evenly divide another number, while multiples are products of a number multiplied by an integer.
- Range: Factors of a number are finite and limited to numbers less than or equal to itself. Multiples extend infinitely, getting larger.
- Role in Math: Factors decompose numbers into simpler elements, while multiples explore the expansion of numbers.
Understanding these differences is crucial for grasping their unique roles in mathematics.
Importance in Math
Factors and multiples are foundational in various mathematical operations and problem-solving. Their importance is highlighted in:
- Fractions: Simplifying fractions by identifying common factors.
- Least Common Multiple (LCM): Finding the smallest number that is a multiple of two or more numbers.
- Greatest Common Divisor (GCD): Determining the largest number that is a factor of two or more numbers.
These applications demonstrate the versatility and necessity of understanding factors and multiples in a wide range of mathematical contexts.
Calculation Techniques
For Factors
Tips and Tricks
Calculating factors efficiently can save time and enhance understanding of number properties. Prime factorization stands out as a powerful method. Here’s how you can leverage it:
- Use a Factor Tree: Break down a number into its prime factors by dividing it by the smallest prime number possible and continue the process with the quotient until you reach 1.
- Divisibility Rules: Familiarize yourself with rules for divisibility to quickly identify obvious factors without extensive calculation.
- Sieve of Eratosthenes: For larger numbers, using this ancient algorithm can help identify all prime numbers up to a certain limit, aiding in prime factorization.
Prime Factorization
A deeper look into prime factorization shows its utility in breaking down numbers into their simplest form, making it easier to identify common factors between numbers, a key step in simplifying fractions or finding the Greatest Common Divisor (GCD).
For Multiples
Finding Multiples
To find multiples of a number, the process is straightforward but can be optimized with a few strategies:
- Sequential Multiplication: Start with the number itself and keep adding it to get the next multiple.
- Skip Counting: This is effective for small numbers, where you can simply count by the number to get its multiples.
Least Common Multiple (LCM)
Calculating the LCM involves:
- Prime Factorization: Break down the numbers into their prime factors.
- Highest Power Rule: For each prime factor, take the highest power found in the factorization of either number.
- Multiply: Combine these prime factors to get the LCM.
This technique is particularly useful in finding the smallest number that two or more numbers can divide into, crucial for solving problems involving fractions and algebraic expressions.
Factors and Multiples in Algebra
Polynomials
Factors and multiples play a critical role in understanding and manipulating polynomials. Factoring polynomials involves finding the polynomial’s roots, which are, in essence, the factors of the polynomial equation. This process simplifies complex polynomials, making them easier to evaluate and integrate with other algebraic operations.
Equations and Inequalities
Factors and multiples provide a foundation for solving equations and inequalities by:
- Simplifying Equations: Breaking down complex equations into simpler, factorable components.
- Identifying Solutions: Utilizing the zero-product property, where if a product of factors equals zero, at least one of the factors must be zero.
- Divisibility Analysis: Applying divisibility to inequalities for simplification and solution.
Educational Strategies
Teaching Factors and Multiples
Effective teaching strategies include:
- Interactive Tools: Use visual aids and interactive software to illustrate the concepts.
- Real-Life Applications: Connect lessons to real-life scenarios to enhance understanding and retention.
- Incremental Difficulty: Start with basic examples and gradually introduce more complexity.
Learning Challenges
Students often face challenges such as:
- Confusion Between Concepts: Clarify differences and connections through examples.
- Overwhelm with Large Numbers: Introduce strategies to break down and simplify tasks.
- Application Difficulties: Provide ample practice with varied problems to solidify understanding.
Advanced Concepts
Prime Factorization
Exploring prime factorization further reveals its utility in various mathematical fields, including cryptography, where it underpins the security of modern encryption algorithms due to the difficulty of factoring large prime numbers.
LCM and GCD
Understanding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD) deepens one’s ability to solve complex mathematical problems, optimize algorithms, and understand number theory. Their calculation is essential in areas ranging from simplifying fractions to determining periodic events’ synchronization.
Applications Beyond Math
Coding and Algorithms
In computer science, factors and multiples are used in algorithm design for tasks like hashing, memory allocation, and for optimizing searches and sorts. Recognizing patterns in data structures often relies on principles related to factors and multiples.
Everyday Life
Factors and multiples find application in daily activities such as:
- Cooking: Adjusting recipes based on serving size requires understanding multiples.
- Scheduling: Organizing events without conflicts involves calculating common multiples and factors.
- DIY Projects: Measurements and material quantities often rely on understanding these concepts for efficient use and minimal waste.
Frequently Asked Questions
What are factors?
Factors of a number include all the whole numbers that can be evenly divided into that number. For example, the factors of 6 are 1, 2, 3, and 6. These are the numbers that divide 6 without leaving a remainder, showcasing the numbers’ basic building blocks.
How are multiples determined?
Multiples of a number are found by multiplying the number with integers. For instance, the first few multiples of 3 are 3, 6, 9, 12, and so on. These numbers are the result of multiplying 3 by 1, 2, 3, 4, respectively, illustrating the concept of repeated addition.
Why are factors and multiples important?
Understanding factors and multiples is crucial for solving a wide range of mathematical problems, including those involving fractions, divisibility, and algebraic expressions. This knowledge aids in simplifying equations, finding common denominators, and understanding number properties, making it indispensable in both academic and real-world applications.
Can a number be a factor and multiple of itself?
Yes, every non-zero number is both a factor and a multiple of itself. This is because any number divided by itself gives a quotient of one, fulfilling the criteria for being a factor, and when multiplied by one, it produces itself, meeting the criteria for being a multiple.
Conclusion
The intricate relationship between factors and multiples underpins many aspects of mathematics, offering a window into the structured and interconnected nature of numbers. This foundation not only enhances our ability to navigate mathematical challenges but also enriches our understanding of the world through the lens of mathematics. By grasping these concepts, learners and practitioners alike can unlock new levels of insight and problem-solving abilities.
Recognizing the importance of factors and multiples goes beyond academic interest, extending into practical applications that affect various fields, including technology, science, and engineering. As we continue to explore and apply these fundamental concepts, we further our collective ability to innovate, solve complex problems, and appreciate the elegance and efficiency of mathematical relationships.

