In the realm of mathematics, identifying the highest point of a function, whether it’s within a specific range or over its entire domain, is a critical skill. This distinction between the highest points is encapsulated in the concepts of relative and absolute maximum. These terms, while closely related, serve different purposes in mathematical analysis and have unique implications for how we understand and apply mathematical concepts.
The difference between a relative and an absolute maximum lies in their scope of comparison. A relative maximum refers to a point that is higher than the points immediately surrounding it, but not necessarily the highest point over the entire domain of the function. In contrast, an absolute maximum is the highest point across the entire domain of the function, unmatched by any other point.
Focusing on these differences illuminates the nuanced ways mathematicians, engineers, and economists analyze trends, make predictions, and solve optimization problems. The ability to distinguish between these types of maximum values is not just a mathematical exercise; it is a fundamental tool that enhances our understanding of the natural and social sciences.
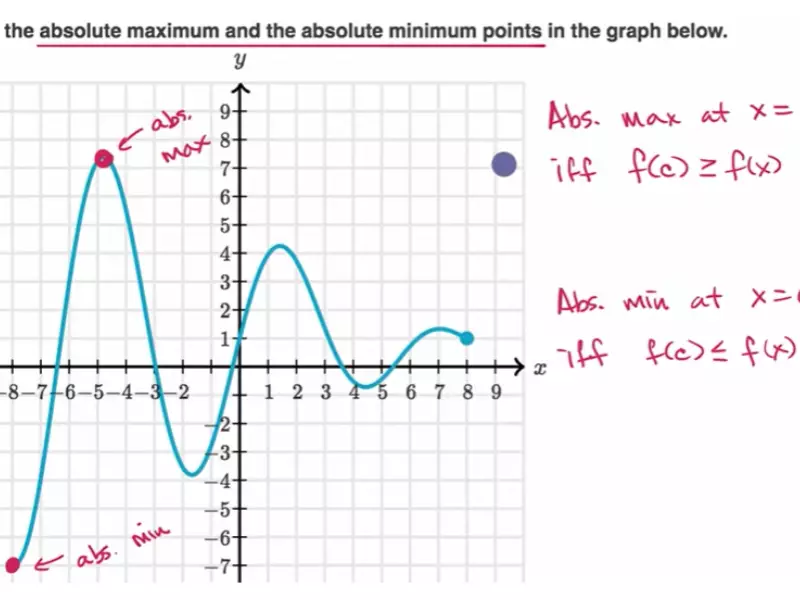
Basics of Maximum Values
Definitions
What is a Maximum Value?
A maximum value in mathematics is a point at which a function reaches its highest value in a given interval or across its entire domain. This peak point can signify the greatest output of a function, representing a pivotal concept in both simple and complex mathematical analyses.
Relative Maximum
A relative maximum refers to a point where a function’s value is higher than that of the points directly surrounding it. It’s a local summit within a specific range, not necessarily the highest point across the entire domain of the function.
Absolute Maximum
An absolute maximum, in contrast, is the highest point over the entire domain of a function. This is the ultimate peak that the function achieves, with no other value exceeding this point across its entire scope.
Key Characteristics
Identifying Features of Relative Maximum
The key to identifying a relative maximum includes observing:
- A change in the direction of the function from increasing to decreasing.
- The value at the relative maximum is higher than the values immediately before and after it.
These characteristics help pinpoint local peaks, essential for analyzing functions’ behaviors within specific intervals.
Identifying Features of Absolute Maximum
To identify an absolute maximum, look for:
- The highest value that a function attains over its entire domain.
- A comparison across all possible values of the function to find the single highest point.
This feature is crucial for understanding the overall maximum output or behavior a function can exhibit.
Comparative Analysis
Similarities
Role in Mathematical Analysis
Both relative and absolute maximums play significant roles in mathematical analysis. They are fundamental in studying functions, understanding their behavior, and applying this knowledge in various mathematical fields.
Usage in Various Fields
These concepts are not confined to pure mathematics. Fields like engineering, physics, economics, and data science frequently utilize the understanding of maximum values to solve problems, optimize systems, and predict future trends.
Differences
Conceptual Distinctions
The main difference lies in their scope:
- Relative maximum is about local peaks within a restricted range.
- Absolute maximum refers to the highest point across the entire domain.
Practical Examples
To illustrate, consider a landscape with multiple hills and valleys. A relative maximum could represent the top of a small hill, while the absolute maximum would be the highest mountain peak in the entire range.
Calculation Methods
Finding Relative Maximum
Graphical Method
- Plot the function on a graph.
- Look for points where the graph changes direction from increasing to decreasing.
- These points are potential relative maximums.
This visual approach is intuitive and helps identify local maxima quickly.
Calculus Approach
- Calculate the first derivative of the function.
- Find points where the derivative changes sign from positive to negative.
- Evaluate the second derivative to confirm a maximum at these points.
This method provides a precise mathematical technique to find relative maximums.
Finding Absolute Maximum
Closed Interval Method
- Identify the domain of the function, ensuring it is closed and bounded.
- Calculate the function’s values at critical points and endpoints.
- The highest of these values is the absolute maximum.
This method is reliable for functions defined on closed intervals.
Analytical Method
- Analyze the function across its entire domain.
- Use calculus to find critical points and evaluate their values.
- Compare these values to determine the highest point.
The analytical method is comprehensive, allowing for the identification of the absolute maximum over an entire domain, including infinite intervals.
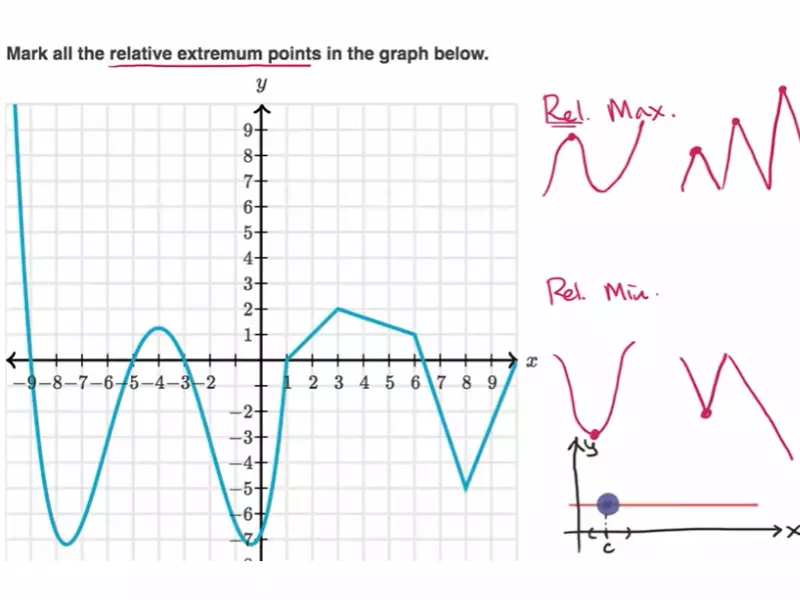
Applications
In Mathematics
Calculus and Optimization Problems
In calculus, the concepts of relative and absolute maximums are pivotal for solving optimization problems. Optimization involves finding the best solution from a set of feasible solutions. Here’s how these concepts apply:
- Calculus: By differentiating a function and finding its critical points, mathematicians can determine where a function might achieve maximum values. These critical points are then analyzed to identify whether they are relative maxima or the absolute maximum.
- Optimization Problems: In real-world scenarios, such as minimizing cost or maximizing efficiency, identifying the absolute maximum or minimum values of a function is essential. For instance, businesses use these concepts to optimize profit margins and operational efficiency.
Graphical Interpretations
Graphical interpretations of functions provide a visual way to understand the behavior of mathematical models. By plotting a function on a graph, one can visually identify relative and absolute maximum points. This method is particularly useful in educational settings, where visual aids can help students grasp complex concepts more intuitively.
Beyond Mathematics
Engineering Applications
In engineering, the principles of maximum values are applied in the design and analysis of systems and structures.
- Structural Engineering: Identifying stress points in materials and structures involves calculating maximum values to ensure safety and durability.
- Electrical Engineering: In circuit design, engineers often seek to optimize signal strength at specific points, requiring an understanding of maximum values to enhance performance.
Economic Models
Economic models frequently incorporate the use of maximum values to predict market behaviors and optimize economic outcomes.
- Market Analysis: Economists analyze peaks and troughs in market data to predict future trends. Identifying relative maxima can help in understanding short-term market movements, while absolute maxima are useful for long-term predictions.
- Resource Allocation: In the context of limited resources, understanding how to maximize output or efficiency is crucial. Economic models use these mathematical concepts to develop strategies for optimal resource distribution.
Challenges and Solutions
Common Mistakes
Misidentification of Types
One common mistake is confusing relative maximums with absolute maximums. This confusion can lead to incorrect conclusions in both mathematical analysis and practical applications.
- Solution: Emphasize the contextual differences between local (relative) and global (absolute) maxima. Clear definitions and examples can help distinguish between these concepts.
Overlooking Conditions
Another mistake is overlooking the conditions that define the domain or range within which a maximum is sought. This oversight can invalidate the identification of a true maximum value.
- Solution: Always consider the domain and constraints of a problem. Understand the conditions under which the function operates to accurately identify maximum values.
Tips for Accurate Identification
Analytical Checks
Performing analytical checks involves using calculus and other mathematical tools to confirm the nature of maximum points.
- Steps:
- Differentiate the function to find critical points.
- Use the second derivative test or other analytical methods to determine the nature of these points.
- Ensure that the points meet the criteria for relative or absolute maxima within the given domain.
This methodical approach minimizes errors and ensures accurate identification of maximum values.
Utilizing Technology
Modern technology offers powerful tools for identifying maximum values accurately and efficiently.
- Software and Applications: Tools like MATLAB, Mathematica, and various graphing calculators can automate the process of finding maximum values. They provide precise calculations and graphical representations that aid in analysis.
- Online Platforms: Online resources and platforms offer interactive tutorials and problem-solving tools that can help understand and apply the concepts of maximum values in various contexts.
By leveraging technology, individuals can enhance their analytical capabilities and achieve more accurate results in both theoretical and practical applications.
Frequently Asked Questions
What is a Relative Maximum?
A relative maximum is a point on a graph where the function’s value is higher than all other values in the immediate vicinity. It’s like standing on the highest hill in a small neighborhood of hills, but not necessarily on the highest mountain in the entire region. This concept is crucial in identifying local peaks within a specific range of a function.
How is an Absolute Maximum Defined?
An absolute maximum is the highest point across the entire domain of a function. It’s akin to standing on the highest mountain peak in an entire country, where no other peak exceeds this height. This value is essential for understanding the overall behavior of a function and for solving optimization problems across the entire range of interest.
Why are Relative and Absolute Maximums Important?
Understanding relative and absolute maximums is vital for solving complex problems in calculus, physics, engineering, and economics. These concepts help in optimizing functions, predicting outcomes, and making informed decisions based on the analysis of data trends. They are foundational tools in the mathematician’s toolkit, enabling precise analysis and application of mathematical theories in real-world scenarios.
Conclusion
The concepts of relative and absolute maximum are more than mere mathematical jargon; they are essential tools that enable us to analyze, predict, and optimize various phenomena in the natural and social sciences. Their application extends beyond the confines of mathematics, influencing decision-making processes in fields as diverse as engineering, economics, and environmental science.
Recognizing the difference between these two types of maximum values enhances our ability to approach problems with nuanced understanding and sophisticated analytical skills. It empowers us to dissect complex scenarios, paving the way for innovation and discovery across multiple disciplines. As we continue to explore the vast landscape of mathematics and its applications, the distinction between relative and absolute maximum remains a beacon of clarity in our pursuit of knowledge and understanding.
