Have you ever heard of point groups and space groups and wondered what the difference between them is? Point groups and space groups are both used to describe the symmetry of crystals, and while they are related, they are not the same. In this blog, we will explore the difference between point groups and space groups and how they are used in crystallography.
In this blog, we will explore the difference between point groups and space groups and how they are used in crystallography.
Understanding the difference between point groups and space groups
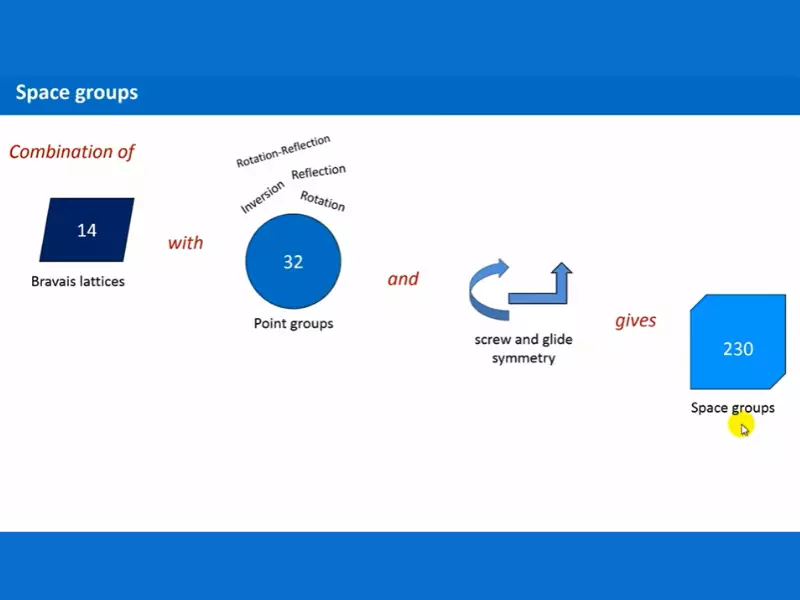
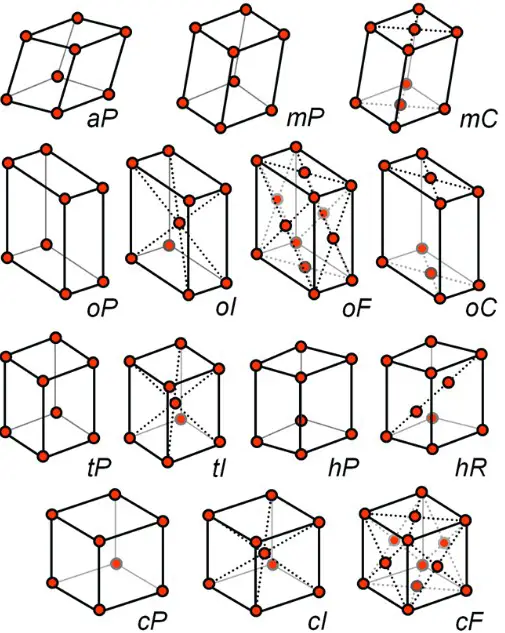
Understanding the difference between point groups and space groups can be a little confusing. To help clarify, point groups are symmetries of a single molecule or atom, while space groups are symmetries of a crystal lattice. Both point and space groups can be defined by the symmetry operations they contain.
Both point and space groups can be defined by the symmetry operations they contain. Point groups focus on the symmetries of the molecule or atom while space groups also consider the translations of the lattice. Point group and space group operations are related, as a point group can form a space group when translations are added.
To summarize, point groups are the symmetries of a single molecule, while space groups are the symmetries of a crystal lattice that are formed from point group operations plus translations.
Exploring the symmetry of point groups
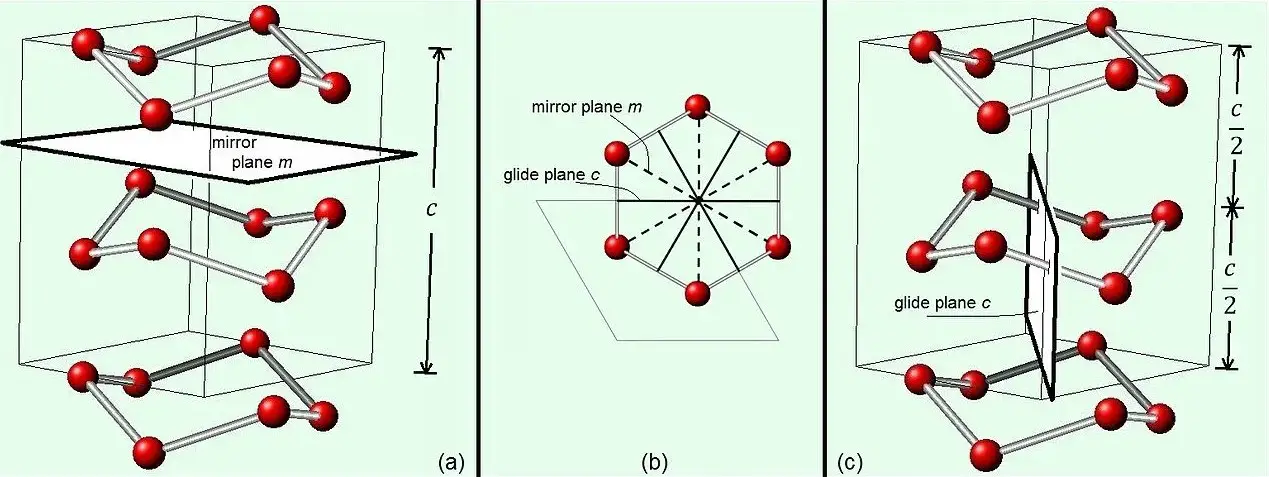
Point groups and space groups are two important concepts when it comes to symmetry in crystallography. While point groups refer to the symmetry of a crystal lattice in three-dimensional space, space groups take this a step further and consider how the lattice interacts with the planes that contain it. Point groups are characterized by the symmetry elements they contain, such as rotations, reflections and inversions, while space groups are determined by operations such as translations and glide planes.
Point groups are characterized by the symmetry elements they contain, such as rotations, reflections and inversions, while space groups are determined by operations such as translations and glide planes.
The difference between point groups and space groups is that point groups only consider the symmetry of the crystal lattice, while space groups account for the lattice’s interaction with the planes that contain it. This allows for a much more comprehensive understanding of the symmetry of a crystal structure.
Exploring the symmetry of space groups
Space groups are one of the most fascinating and mysterious symmetries of nature. They provide a way to describe the arrangement of atoms in a crystal structure and can be used to predict the properties of materials. The difference between point groups and space groups lies in the dimensionality of the symmetries they describe.
The difference between point groups and space groups lies in the dimensionality of the symmetries they describe. Point groups are two-dimensional symmetries, meaning they describe the symmetries of a plane, while space groups are three-dimensional, meaning they describe the symmetries of a three-dimensional space. Each space group contains a set of point groups which can be used to describe the symmetry of the space group as a whole.
Exploring the symmetry of space groups can provide valuable insights into the properties of materials and the behavior of atoms in a crystal structure.
Comparing point groups and space groups
Point groups and space groups are two key concepts in crystallography. While they both relate to the symmetry of crystals, there are some important differences to be aware of when comparing the two.
Point groups describe how the symmetry of a crystal looks from the point of view of an observer at a single point, while space groups consider the symmetry of the entire crystal structure. Point groups focus on symmetry elements such as rotations and reflections, while space groups also consider translations, which describe how the symmetry is repeated in the three-dimensional space.
Thus, while point groups are a useful tool for describing the symmetries of a single crystal, space groups are better suited for describing the symmetries of an entire crystal lattice.
Examples of point groups and space groups
Point groups and space groups are two categories of symmetry in crystallography. Point groups are the symmetries of a single point and space groups are the symmetries of a three-dimensional space. The main difference between the two is that point groups consist of rotational and reflectional symmetry while space groups also include translational symmetry.
Point groups are used to classify crystals according to their crystal structure, while space groups are used to describe how atoms are arranged in a crystal. While both types of symmetry are related, their applications are distinct.
Point groups are used to describe the symmetry of individual molecules, while space groups are used to describe the symmetry of entire crystals.
Conclusion
In conclusion, the difference between a point group and a space group is that a point group is a symmetry operation that acts on a single point in a molecule, while a space group is a symmetry operation that applies to a three-dimensional crystal lattice. Point groups are used to describe the symmetry of a molecule, while space groups are used to describe the symmetry of a crystal lattice.