Chemical equations serve as the shorthand of the laboratory, translating the complex world of atomic and molecular interactions into a language that is universally understood by chemists. These equations are more than just notations; they are the backbone of understanding chemical reactions, allowing scientists to predict the outcomes of experiments, understand the conservation of mass, and quantify reactants and products.
The difference between balanced and skeleton equations lies at the heart of chemical documentation and experimentation. A skeleton equation outlines the reactants and products of a chemical reaction without regard to the quantities involved, while a balanced equation ensures that the law of conservation of mass is respected by adjusting coefficients to ensure that the same number of each type of atom appears on both sides of the equation.
Balanced equations are crucial for conducting accurate experiments and quantifying chemical reactions, as they provide the exact proportions of reactants required to achieve a complete reaction without excess. Skeleton equations, on the other hand, are often the first step in the process, offering a preliminary view before the detailed balancing work is undertaken. Understanding both forms and their interplay is essential for students, researchers, and professionals in the field of chemistry.
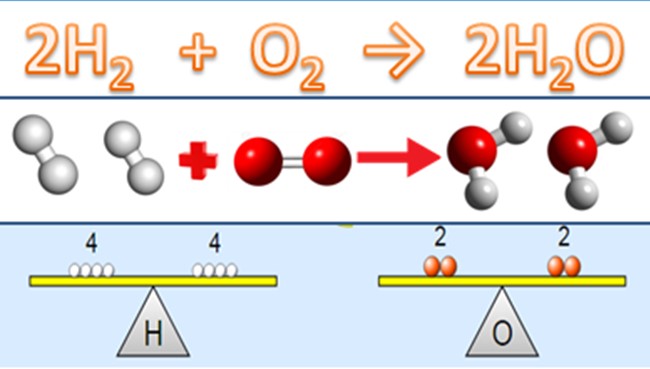
Chemical Equations Basics
Definition of a Chemical Equation
At its core, a chemical equation is a written representation of a chemical reaction. It depicts the reactants (substances that start the reaction) on the left side and the products (substances formed by the reaction) on the right side, with an arrow pointing from reactants to products to indicate the direction of the reaction. This notation is critical for scientists to communicate complex chemical processes in a clear, concise manner.
Roles and Examples
Chemical equations serve several essential roles in the field of chemistry:
- Predicting Products: They allow chemists to predict the outcome of a reaction, helping in planning experiments and analyzing results.
- Quantitative Analysis: Equations provide a basis for calculating the amounts of reactants and products involved in a chemical reaction, essential for stoichiometry.
- Teaching Tool: They are fundamental in educational settings, helping students understand reaction mechanisms and the conservation of mass.
Example: The combustion of methane can be represented as: ��4+2�2→��2+2�2�CH4+2O2→CO2+2H2O This equation shows methane reacting with oxygen to produce carbon dioxide and water.
Skeleton Equations
Definition and Features
A skeleton equation is a basic form of a chemical equation. It lists the chemical formulas of the reactants and products but does not specify the quantities needed to balance the reaction. Think of it as a rough draft or an outline of the reaction, where the details regarding the balance of atoms are yet to be filled in.
Characteristics of Skeleton Equations
Skeleton equations are characterized by:
- Lack of Coefficients: They do not include coefficients indicating the quantity of each substance.
- Unbalanced Form: Because they lack coefficients, skeleton equations often do not obey the law of conservation of mass out of the box.
Examples
An example of a skeleton equation is the reaction between iron (Fe) and sulfur (S) to form iron(II) sulfide (FeS): ��+�→���Fe+S→FeS This equation simply lists the reactants and the product without specifying their amounts.
Balanced Equations
Definition and Significance
A balanced equation, in contrast, is a chemical equation in which the number of atoms for each element in the reaction and the total charge are the same on both the reactants’ and the products’ sides. This balance is crucial as it reflects the law of conservation of mass, stating that mass cannot be created or destroyed in a chemical reaction.
Characteristics of Balanced Equations
The key features of balanced equations include:
- Coefficients: Numbers placed before the chemical formulas to indicate the quantity of each substance.
- Conservation of Mass: The equation must balance to ensure that the same amount of matter exists before and after the reaction.
- Stoichiometric Relationships: Balanced equations allow for the calculation of reactant and product amounts in a reaction, facilitating stoichiometry.
Examples
Balancing the previously mentioned combustion of methane yields: ��4+2�2→��2+2�2�CH4+2O2→CO2+2H2O This balanced equation indicates that one methane molecule reacts with two oxygen molecules to produce one carbon dioxide molecule and two water molecules, adhering to the conservation of mass.
Key Differences
Chemical Representation
- Skeleton Equations: Represent only the form of the reaction with the reactants and products listed.
- Balanced Equations: Provide a quantitative representation that respects the conservation of mass.
Complexity and Completeness
- Skeleton Equations: Are simpler but incomplete, as they don’t reflect the mass balance.
- Balanced Equations: Are more complex due to the inclusion of coefficients, but they offer a complete picture of the reaction, including the stoichiometry.
Role in Chemical Reactions
- Skeleton Equations: Serve as the preliminary step in formulating a chemical equation, useful for identifying the reactants and products.
- Balanced Equations: Essential for the practical application of chemistry, including experimental design and quantitative analysis.
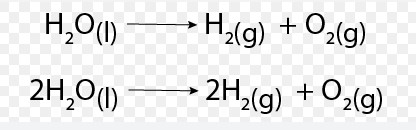
Balancing Techniques
Overview of Balancing Methods
Balancing chemical equations is a fundamental skill in chemistry, ensuring that the law of conservation of mass is respected in chemical reactions. The process involves adjusting coefficients in front of compounds to make sure the number of atoms for each element is the same on both sides of the equation. There are several methods for balancing equations, including the trial and error method, the algebraic method, and the inspection method. Each technique has its applications, with some being more suited to straightforward equations and others designed for handling more complex scenarios.
Steps for Balancing Equations
Balancing a chemical equation typically follows a structured approach. Here’s a simplified step-by-step guide to using the inspection method, one of the most commonly taught techniques:
- List all elements involved in the reaction on both sides of the equation.
- Count the atoms of each element in the reactants and products.
- Start with complex molecules or the element that appears in the least number of reactants and products.
- Adjust coefficients to balance the atoms, starting with the most complex molecule.
- Iterate through each element, adjusting coefficients as necessary until each element has the same number of atoms on both sides.
- Finalize the equation to ensure all coefficients are in the simplest whole number ratios.
Tips and Tricks
- Balance polyatomic ions as a whole when they appear unchanged on both sides of the equation.
- Leave hydrogen and oxygen for last as they are often the most flexible in terms of balancing.
- Check your work by recounting the atoms of each element on both sides of the equation.
Importance in Chemistry
Role in Stoichiometry
Balanced equations are vital for stoichiometry, the branch of chemistry that deals with the quantitative relationships between reactants and products in a chemical reaction. By providing the exact ratios of substances involved, balanced equations allow chemists to calculate how much of each reactant is needed to produce a desired amount of product, making them indispensable tools in both laboratory and industrial settings.
Impact on Chemical Research and Industry
In chemical research, balanced equations are foundational for predicting reaction outcomes, synthesizing new compounds, and understanding reaction mechanisms. They enable scientists to design experiments methodically, reduce waste, and optimize reaction conditions.
In industry, balanced equations guide the scaling of chemical processes from the laboratory to production level, ensuring that chemical reactions are economically viable and environmentally sustainable. Industries ranging from pharmaceuticals to petrochemicals rely on accurately balanced equations to maintain efficiency, safety, and regulatory compliance.
Common Challenges
Issues with Complex Reactions
Balancing equations becomes significantly more challenging as the complexity of the reactions increases. Complex reactions may involve multiple steps, intermediates, and side reactions, each requiring careful consideration to balance accurately. Some common issues include:
- Polyatomic ions that may change throughout the reaction.
- Multiple solutions where more than one set of coefficients can balance the equation.
- Redox reactions, where electron transfers complicate the balancing process.
Strategies for Overcoming Difficulties
Despite these challenges, several strategies can facilitate the balancing of complex equations:
- Identify and balance the redox pairs first in oxidation-reduction reactions, using the oxidation numbers to guide you.
- Use the algebraic method for reactions that defy simple inspection, setting up equations for each element and solving for the coefficients.
- Practice regularly with increasingly complex equations to build familiarity and intuition.
- Seek help when stuck, utilizing resources like textbooks, online forums, and educational software that can provide hints or solutions.

Frequently Asked Questions
What is a Chemical Equation?
A chemical equation is a symbolic representation of a chemical reaction, showing the reactants on the left, the products on the right, and the direction of the reaction. It provides a concise way for chemists to convey information about the chemical changes occurring during the reaction.
Why Balance Chemical Equations?
Balancing chemical equations is necessary to adhere to the law of conservation of mass, ensuring that the same number of atoms for each element is present on both sides of the equation. This process is crucial for accurately predicting the quantities of reactants and products involved in a chemical reaction.
How Do You Balance a Skeleton Equation?
Balancing a skeleton equation involves adding coefficients to the reactants and products to ensure that the number of atoms for each element is the same on both sides of the equation. This process often requires iterative adjustments to achieve a fully balanced equation.
What Makes a Balanced Equation Different from a Skeleton Equation?
A balanced equation differs from a skeleton equation in that it includes coefficients that ensure the law of conservation of mass is satisfied, with an equal number of atoms for each element on both sides of the equation. Skeleton equations, meanwhile, simply list the reactants and products without regard to their quantities.
Conclusion
The distinction between balanced and skeleton equations is a fundamental concept in chemistry that underpins the accurate description and execution of chemical reactions. Through the careful balance of atoms and molecules, scientists ensure that their work adheres to the unchanging laws of physics, particularly the conservation of mass. This understanding not only facilitates successful laboratory experiments but also supports the theoretical framework of chemical interactions.
Grasping the nuances between these two types of equations empowers students and professionals alike to approach chemical equations with the precision and accuracy required for scientific inquiry and industrial application. It is a critical skill that enhances one’s ability to predict, perform, and analyze chemical reactions, thereby contributing to advancements in research and technology.
